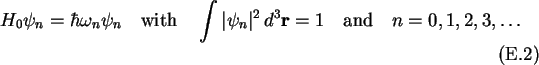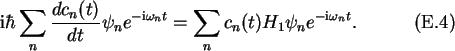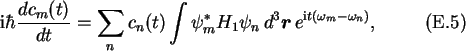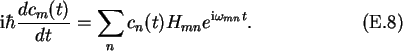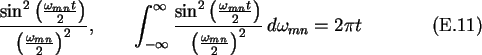Next: F Second Order Co
Up: Dissertation Christoph Wasshuber
Previous: D Integration of Fermi
E Fermi's Golden Rule
The time dependent Schrödinger Equation can be written as
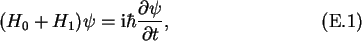
where H1 is a small perturbation to the Hamiltonian H0. The solution
of the unperturbed case is
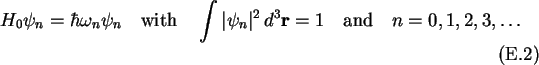
The eigenvalues are
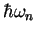 ,
and the orthonormal eigenfunctions are
,
and the orthonormal eigenfunctions are
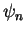 .
Under the assumption that the perturbation H1 is small, the wave function
for the perturbed case can be expanded in a series of the orthonormal
wave functions of the unperturbed case [29].
.
Under the assumption that the perturbation H1 is small, the wave function
for the perturbed case can be expanded in a series of the orthonormal
wave functions of the unperturbed case [29].
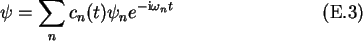
Inserting (E.3) into the time dependent
Schrödinger equation (E.1), and using
(E.2) gives
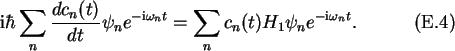
If this is multiplied by
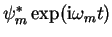 ,
and integrated
over the volume one obtains
,
and integrated
over the volume one obtains
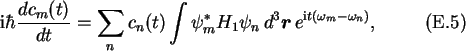
since orthonormality makes

which vanishes for 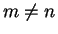 and equals unity for m=n. With the definitions
and equals unity for m=n. With the definitions
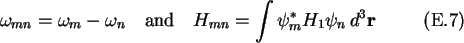
one can write (E.5) as
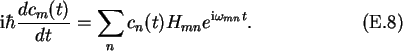
In general, when the perturbation is turned on at t=0, it may be assumed
that the system is in state m at t=0, and cm(0)=1, while cn(0)=0for all other states. Furthermore, it is assumed that the scattering out of the
initial state is small, so that cm(t)=1 for all time. This assumption
neglects the conservation of particles.
Considering these assumptions, one
can solve (E.8).
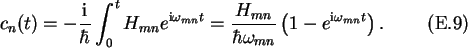
The probability of occupying state n is then
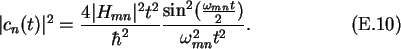
For times
 ,
which are long enough such that the scattering
process has been completed, the function
,
which are long enough such that the scattering
process has been completed, the function
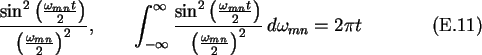
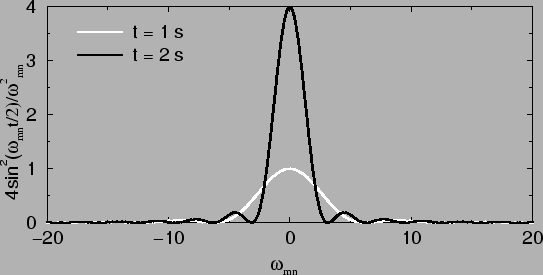
has the property of a 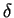 -function (see Fig. E.1).
-function (see Fig. E.1).
Figure:
The function
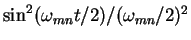 has the
property of a
has the
property of a
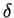 -function.
-function.
 |
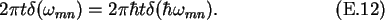
The transition probability per unit time, the
transmission rate, is then
given by the so called Fermi Golden Rule
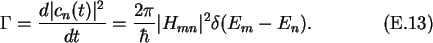
This means that a scattering process, in our case a tunnel event, only takes
place if the energy of the particle is conserved, Em = En.




Next: F Second Order Co
Up: Dissertation Christoph Wasshuber
Previous: D Integration of Fermi
Christoph Wasshuber