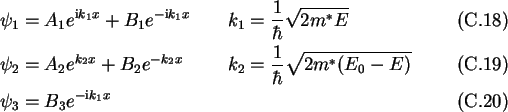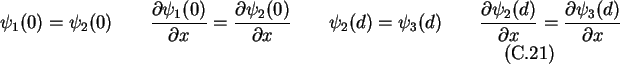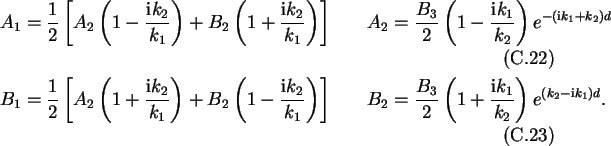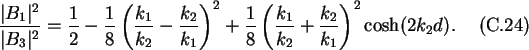Next: D Integration of Fermi Up: C Solutions to Schrödinger's Previous: C.2 The Finite Potential

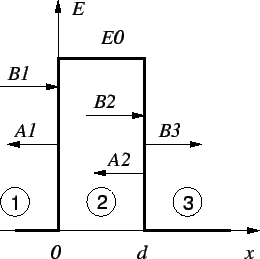
C.3 The Rectangular Potential Barrier

We calculate the tunnel transmission coefficient for an electron wave packet which hits the rectangular potential barrier with height E₀ and width d (see Fig. C.3).

**Figure C.3:** Tunneling through a rectangular barrier with width d and height E₀.
$\includegraphics{rectangular_barrier.eps}$

Starting with an Ansatz for the three regions
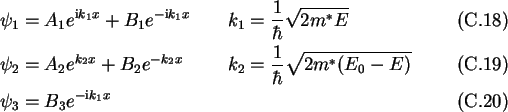
$\begin{alignat}{2} \psi_1 &= A_1e^{\text{i}k_1x}+B_1e^{-\text{i}k_1x} &\qquad k_... ...ac{1}{\hbar} \sqrt{2m^*(E_0-E)}\\ \psi_3 &= B_3e^{-\text{i}k_1x} \end{alignat}$
and the boundary conditions
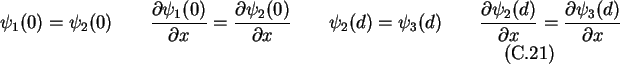
$\begin{gather}\psi_1(0) = \psi_2(0) \qquad \frac{\partial\psi_1(0)}{\partial x} ... ...rtial\psi_2(d)}{\partial x} = \frac{\partial\psi_3(d)}{\partial x} \end{gather}$
one obtains
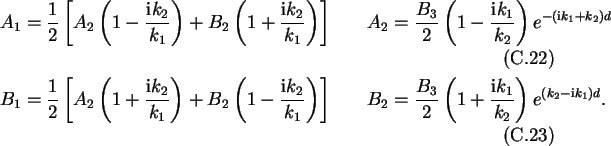
$\begin{alignat}{2} A_1 &= \frac{1}{2}\left[A_2\left(1-\frac{\text{i}k_2}{k_1}\ri... ...3}{2}\left(1+\frac{\text{i}k_1}{k_2}\right)e^{(k_2-\text{i}k_1)d}. \end{alignat}$
The ratio of incoming and transmitted probability amplitude is
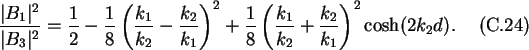
$\begin{gather}\frac{\vert B_1\vert^2}{\vert B_3\vert^2}=\frac{1}{2}-\frac{1}{8}\... ...{1}{8}\left(\frac{k_1}{k_2}+ \frac{k_2}{k_1}\right)^2\cosh(2k_2d). \end{gather}$
The transmission probability depends exponentially on thickness and height of the barrier.

Christoph Wasshuber