



Next: G Rational Padé Approximations
Up: Dissertation Christoph Wasshuber
Previous: E Fermi's Golden Rule
F Second Order Co Tunneling Rate at Zero Temperature
The second order co-tunneling rate can be calculated analytically for zero temperature.
Starting from (2.44) for N=2, the co-tunneling rate may be written as
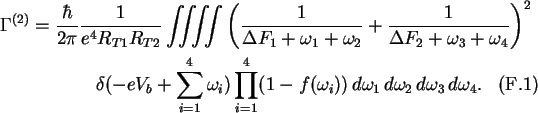
At zero temperature the Fermi functions are either zero or one and may
therefore be moved in the boundaries of the integrals.
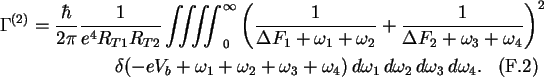
The integration over 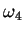 is eliminated by the
is eliminated by the 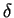 -function.
The condition
-function.
The condition
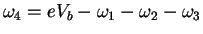 demanded by the
demanded by the
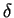 -function and the integration regions of
-function and the integration regions of
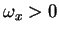 give
the inequalities
give
the inequalities
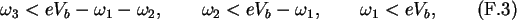
for the new upper boundaries of integration.
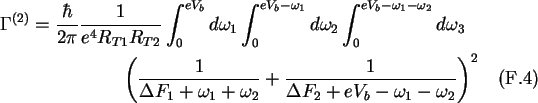
Integrating over 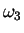 results in
results in
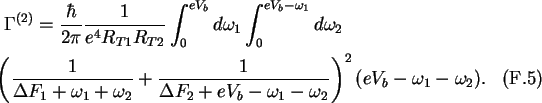
Substituting
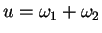 gives
gives
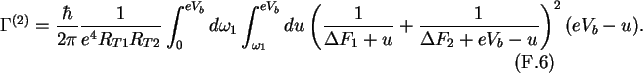
The integrand can be changed to a partial sum
![\begin{multline}\Gamma^{(2)}=\frac{\hbar}{2\pi}\frac{1}{e^4 R_{T1}R_{T2}}
\int_...
...(\frac{1}{\Delta F_1+u}+\frac{1}{\Delta F_2+eV_b-u}\right)\Biggr]
\end{multline}](img450.gif)
![\begin{multline}\Gamma^{(2)}=\frac{\hbar}{2\pi}\frac{1}{e^4 R_{T1}R_{T2}}
\int_...
...{\Delta F_2+eV_b-\omega_1}{\Delta F_2}\right\vert\right)
\Biggr]
\end{multline}](img451.gif)
![\begin{multline}\Gamma^{(2)}=\frac{\hbar}{2\pi}\frac{1}{e^4 R_{T1}R_{T2}}
\Bigg...
...2\ln\left\vert 1+\frac{eV_b}{\Delta F_2}\right\vert\right)\Biggr]
\end{multline}](img452.gif)
And finally collecting the logarithms yields
![\begin{gather}\Gamma^{(2)}\arrowvert_{T=0}=\frac{\hbar V_b}{2\pi e^3R_{T1}R_{T2}...
...n
\left\vert 1+\frac{eV_b}{\Delta F_i}\right\vert\right)-2\right].
\end{gather}](img453.gif)
Christoph Wasshuber
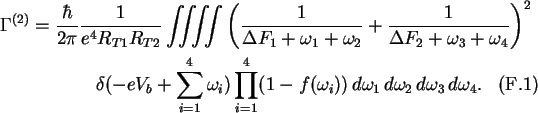
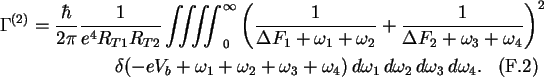
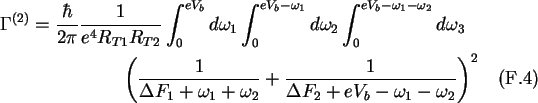
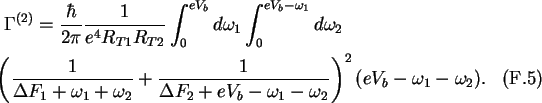
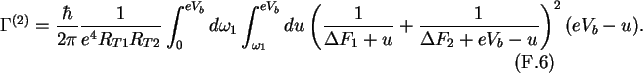
![\begin{multline}\Gamma^{(2)}=\frac{\hbar}{2\pi}\frac{1}{e^4 R_{T1}R_{T2}}
\int_...
...(\frac{1}{\Delta F_1+u}+\frac{1}{\Delta F_2+eV_b-u}\right)\Biggr]
\end{multline}](img450.gif)
![\begin{multline}\Gamma^{(2)}=\frac{\hbar}{2\pi}\frac{1}{e^4 R_{T1}R_{T2}}
\int_...
...{\Delta F_2+eV_b-\omega_1}{\Delta F_2}\right\vert\right)
\Biggr]
\end{multline}](img451.gif)
![\begin{multline}\Gamma^{(2)}=\frac{\hbar}{2\pi}\frac{1}{e^4 R_{T1}R_{T2}}
\Bigg...
...2\ln\left\vert 1+\frac{eV_b}{\Delta F_2}\right\vert\right)\Biggr]
\end{multline}](img452.gif)
![\begin{gather}\Gamma^{(2)}\arrowvert_{T=0}=\frac{\hbar V_b}{2\pi e^3R_{T1}R_{T2}...
...n
\left\vert 1+\frac{eV_b}{\Delta F_i}\right\vert\right)-2\right].
\end{gather}](img453.gif)