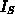 , cell area
, cell area 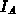 , and
orthogonality
, and
orthogonality 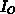 of the numerically generated grid.
of the numerically generated grid.




Variational methods offer a direct influence on certain grid
properties [Bra82]. We minimize a linear combination of three
integrals (3.3-26) to control smoothness 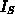 , cell area
, cell area 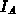 , and
orthogonality
, and
orthogonality 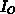 of the numerically generated grid.
of the numerically generated grid.
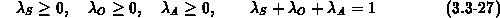
In the orthogonality functional 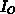 a weighting function
a weighting function 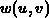 enables
additional orthogonality control at the boundary.
enables
additional orthogonality control at the boundary.
We solve the minimization problem for the overall criterion 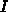 by
calculating the Euler-Lagrange equations for the variational problem
[Bau90]. They are obtained from (3.3-31) and (3.3-32).
by
calculating the Euler-Lagrange equations for the variational problem
[Bau90]. They are obtained from (3.3-31) and (3.3-32).
The functional 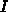 is a linear function of the three integrals
is a linear function of the three integrals 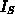 ,
, 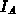 and
and 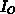 , and therefore we can calculate the Euler-Lagrange equations for
these integrals separately and superimpose them to the final PDEs.
, and therefore we can calculate the Euler-Lagrange equations for
these integrals separately and superimpose them to the final PDEs.
The Euler-Lagrange Equations for the smoothness functional
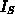 (3.3-28) are (3.3-33) and (3.3-34) using the
abbreviations (3.3-35). For
(3.3-28) are (3.3-33) and (3.3-34) using the
abbreviations (3.3-35). For 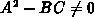 they reduce to (3.3-36) and (3.3-37).
they reduce to (3.3-36) and (3.3-37).
As Euler-Lagrange equations for the area functional 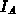 (3.3-29)
we obtain (3.3-38) - (3.3-39).
(3.3-29)
we obtain (3.3-38) - (3.3-39).
The Euler-Lagrange Equations for the orthogonality functional
with included boundary control 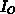 (3.3-30) are
(3.3-40) - (3.3-41) using the substitutions
(3.3-42) - (3.3-43).
(3.3-30) are
(3.3-40) - (3.3-41) using the substitutions
(3.3-42) - (3.3-43).
The resulting PDEs are discretized using nine-point finite differences, the nonlinear algebraic system is solved with a nonlinear SOR algorithm [Ort70].
Figure 3.3-8 shows grids for a test geometry, generated with algebraic, elliptic and variational methods.