



Next: 8.1.1 Entire Layout
Up: 8. Simulation Examples
Previous: 8. Simulation Examples
8.1 Aerial Image Simulation of the Layout of a Multiplexer
The entire layout of the 4:16 multiplexer is shown in
Figure 8.1. The aerial images of the following four layers are
calculated since these layers are of special interest for
lithography (cf. Figure 8.2):
- 1.
- The POLY1 layer defines the transistor channel length and
thus carries the smallest features of all layers.
- 2.
- The ACTIVE-AREA layer defines the transistor width and is together
with POLY1 of crucial importance for a well operating transistor.
- 3.
- The CONTACT layer defines the contacts between POLY1 and METAL1
as well as between ACTIVE-AREA and METAL1. Among all contact and via
layers it has patterns with minimal feature size.
- 4.
- The METAL1 layer is the first metalization layer. Its feature
dimensions are thus minimal of all back-end layers.
The other four layers constituting the overall manufacturing process,
namely N-WELL, P-IMPLANT,
METAL2, and VIA, are omitted since they are less interesting with respect to
lithography. The layout is 52 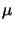 m x 29
m x 29 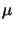 m large, whereas the
smallest pattern is of size 0.25
m large, whereas the
smallest pattern is of size 0.25 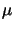 m (cf. Figure 8.1 and
Figure 8.2). The ratio between minimal feature size
and lateral x- and y-extensions of the layout is 208 and 116,
respectively.
m (cf. Figure 8.1 and
Figure 8.2). The ratio between minimal feature size
and lateral x- and y-extensions of the layout is 208 and 116,
respectively.
The stepper is a DUV projection printing system with a wavelength
of 248 nm, a numerical aperture of
NA = 0.6, and a partial coherence
factor of
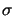 = 0.7. Following the Rayleigh criteria
given in (2.1) and (2.2),
the minimal printable feature
size W and the achievable depth of focus
DOF are approximately
= 0.7. Following the Rayleigh criteria
given in (2.1) and (2.2),
the minimal printable feature
size W and the achievable depth of focus
DOF are approximately
 |
(8.1) |
whereby for the process parameters k1 = 0.6 and k2 = 1.0 are
inserted [11, p. 415]. The stepper is thus capable to print the
0.25 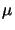 m technology, but the required resolution is already critical.
Therefore the printing tolerance is small, especially the shallow depth of
focus of 690 nm causes problems in a factory floor process.
Advanced lithographic techniques
such as off-axis apertures and phase-shifting masks enhance the performance
considerably. Printing with a reasonably large latitude becomes
feasible without changing the core of the stepper, i.e., the wavelength
of
m technology, but the required resolution is already critical.
Therefore the printing tolerance is small, especially the shallow depth of
focus of 690 nm causes problems in a factory floor process.
Advanced lithographic techniques
such as off-axis apertures and phase-shifting masks enhance the performance
considerably. Printing with a reasonably large latitude becomes
feasible without changing the core of the stepper, i.e., the wavelength
of
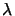 = 248 nm and the numerical aperture of
NA = 0.6 are kept constant. Before we discuss the
simulation results, a few notes on the computational performance of the
aerial image module are given.
= 248 nm and the numerical aperture of
NA = 0.6 are kept constant. Before we discuss the
simulation results, a few notes on the computational performance of the
aerial image module are given.
As can be seen in Figure 8.3 and Figure 8.5 a
57 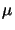 m x 33
m x 33 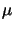 m large simulation area is chosen. The
ortho-product-tensor-grid has 1024(210) ticks in
x-direction, and 512(29) ticks in y-direction.
Approximately 5 grid points per wavelength and thus also per minimal feature
size are used.
The wavevector sampling of (4.56) yields diffraction
orders of
| Nx|max = 136 and
| Ny|max = 79
that are most obliquely incident on the wafer, i.e.,
m large simulation area is chosen. The
ortho-product-tensor-grid has 1024(210) ticks in
x-direction, and 512(29) ticks in y-direction.
Approximately 5 grid points per wavelength and thus also per minimal feature
size are used.
The wavevector sampling of (4.56) yields diffraction
orders of
| Nx|max = 136 and
| Ny|max = 79
that are most obliquely incident on the wafer, i.e.,
 |
(8.2) |
are the largest numbers fulfilling (4.58).
In total 33736 diffraction orders are imaged by the projection lens
since a circular pupil function is assumed, i.e.,

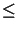 NA. The
originally proposed source discretization using the same high resolution of
NA. The
originally proposed source discretization using the same high resolution of
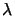 /a
/a 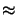 4.39 10-3 and
4.39 10-3 and
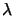 /b
/b 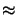 7.58 10-3 would
yield 25321 points (p, q) obeying
7.58 10-3 would
yield 25321 points (p, q) obeying

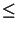 NA
NA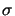 (cf. Figure 4.8). However, it suffices to take every
fourth and second source point in x- and y-direction, respectively, i.e.,
the source sampling rate is set to
sx, p = 4
(cf. Figure 4.8). However, it suffices to take every
fourth and second source point in x- and y-direction, respectively, i.e.,
the source sampling rate is set to
sx, p = 4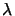 /a and
sy, q = 2
/a and
sy, q = 2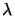 /b.
The aerial image is then built up by the superposition of 2319 coherent
contributions (cf. (4.83)). Memory consumption and
run-time depend on the simulated layers since each of them carries a different
number
NPAT of patterns.
The actual performance figures are summarized in
Table 8.1.
/b.
The aerial image is then built up by the superposition of 2319 coherent
contributions (cf. (4.83)). Memory consumption and
run-time depend on the simulated layers since each of them carries a different
number
NPAT of patterns.
The actual performance figures are summarized in
Table 8.1.
Table 8.1:
Performance
figures of large area aerial image simulation.
The simulations were run on a DEC-600/333 workstation.
| Layer |
NPAT |
NTRI |
Storage |
CPU |
| ACTIVE-AREA |
151 |
1266 |
13 MB |
36 minutes |
| POLY1 |
51 |
440 |
12 MB |
29 minutes |
| CONTACT |
1304 |
2608 |
14 MB |
49 minutes |
| METAL1 |
165 |
1558 |
13 MB |
39 minutes |
|
As can be seen, the storage requirements
only slightly depend on the number of patterns, whereas the dependence of
the run-time is more pronounced. The reason is that the analytical
forward transform of the mask transfer function has to be evaluated for
every pattern, whereas the costs of the
numerical backward transform do not depend on the number of patterns
(cf. Section 4.4). This situation can be quantified
in a simple form by observing from Table 8.1 that the
run-time approximately grows like
![$\displaystyle t_{\mathrm{CPU}}[\mathrm{minutes}] \approx 25.27 + 0.00847\, N_{\mathrm{TRI}},$](img1196.gif) |
(8.3) |
whereby
NTRI is the number of triangles obtained from the
decomposition of the layout into
triangular-shaped patterns (cf. Section 4.4.1).
The first contribution is due to the numerical backward transform and
is constant with respect to the number
NTRI of triangles.
It corresponds for the applied numerical parameters to the minimal
run-time occurring for an ``empty'' layout, i.e.,
tCPU, min = 25.27 minutes. The second term is due to the analytical
forward transform and is thus proportional
to
NTRI. This shows that the analytical forward transform
is advantageous not only because of accuracy but also because of run-time.
However, if the number of triangles exceeds a certain number--in our
example this critical number is
N*TRI 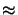 2 980--a numerical
forward transform would be faster since then the analytical algorithm
takes longer than the 25.27 minutes of (8.3).
Aliasing errors are then of course
introduced (cf. Section 4.4.1). Note that the analytical
algorithm can easily be enhanced by searching all equally shaped patterns,
transforming them only once, and multiplying this single transformation
accordingly to the shift-invariance property of the Fourier transformation,
i.e., the basic transformation has to be multiplied with the exponential function
exp(j2
2 980--a numerical
forward transform would be faster since then the analytical algorithm
takes longer than the 25.27 minutes of (8.3).
Aliasing errors are then of course
introduced (cf. Section 4.4.1). Note that the analytical
algorithm can easily be enhanced by searching all equally shaped patterns,
transforming them only once, and multiplying this single transformation
accordingly to the shift-invariance property of the Fourier transformation,
i.e., the basic transformation has to be multiplied with the exponential function
exp(j2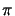 (n
(n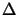 x/a + m
x/a + m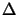 y/b)), whereby
y/b)), whereby 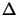 x and
x and 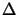 y
refer to the spatial x- and y -offsets of the patterns, respectively.
y
refer to the spatial x- and y -offsets of the patterns, respectively.




Next: 8.1.1 Entire Layout
Up: 8. Simulation Examples
Previous: 8. Simulation Examples
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
![]() m x 29
m x 29 ![]() m large, whereas the
smallest pattern is of size 0.25
m large, whereas the
smallest pattern is of size 0.25 ![]() m (cf. Figure 8.1 and
Figure 8.2). The ratio between minimal feature size
and lateral x- and y-extensions of the layout is 208 and 116,
respectively.
m (cf. Figure 8.1 and
Figure 8.2). The ratio between minimal feature size
and lateral x- and y-extensions of the layout is 208 and 116,
respectively.
![]() = 0.7. Following the Rayleigh criteria
given in (2.1) and (2.2),
the minimal printable feature
size W and the achievable depth of focus
DOF are approximately
= 0.7. Following the Rayleigh criteria
given in (2.1) and (2.2),
the minimal printable feature
size W and the achievable depth of focus
DOF are approximately
![]() m x 33
m x 33 ![]() m large simulation area is chosen. The
ortho-product-tensor-grid has 1024(210) ticks in
x-direction, and 512(29) ticks in y-direction.
Approximately 5 grid points per wavelength and thus also per minimal feature
size are used.
The wavevector sampling of (4.56) yields diffraction
orders of
| Nx|max = 136 and
| Ny|max = 79
that are most obliquely incident on the wafer, i.e.,
m large simulation area is chosen. The
ortho-product-tensor-grid has 1024(210) ticks in
x-direction, and 512(29) ticks in y-direction.
Approximately 5 grid points per wavelength and thus also per minimal feature
size are used.
The wavevector sampling of (4.56) yields diffraction
orders of
| Nx|max = 136 and
| Ny|max = 79
that are most obliquely incident on the wafer, i.e.,