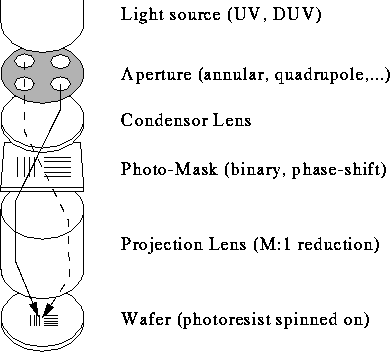
Figure 3: The projection printing system is reduced to its essential parts.
In this section we describe our aerial image simulator.
Although the basic concept follows the vector-valued extension
[7]
[8]
of the scalar theory of Fourier optics
[9],
the module is described in greater length for the following two reasons.
Firstly, the disrectization procedure of the distributed light source
is of crucial importance for a numerically efficient implementation
of the differential method. Secondly, a semi-analytical algorithm
for the computation of the Fourier coefficients of
the mask transmission function is proposed, which has the great advantage of
avoiding aliasing errors due to a sampling of the mask transmission function.
To apply the concept of Fourier optics we first reduce the projection printing system to its essential parts as shown in Fig. 3.

The mask-pattern is thereby assumed to be laterally
periodic with periods
![]() and
and
![]() .
The photomask is infinitesimally thin with ideal
transitions of the transmission characteristic.
The piecewise constant transmission function is
real-valued (zero or one) for binary masks , in case of phase-shift masks
it is complex-valued with module less or equal than one.
.
The photomask is infinitesimally thin with ideal
transitions of the transmission characteristic.
The piecewise constant transmission function is
real-valued (zero or one) for binary masks , in case of phase-shift masks
it is complex-valued with module less or equal than one.
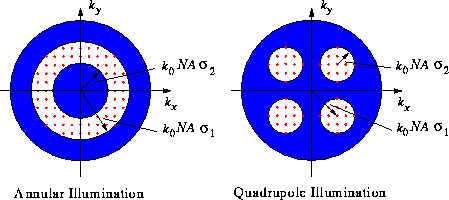
For the simulation of arbitrary illumination forms
the distributed light source
is discretized into mutually independent coherent point sources
![]() .
In
Fig. 4
we show the discretization for an annular and a quadrupole aperture.
.
In
Fig. 4
we show the discretization for an annular and a quadrupole aperture.
We choose the point source locations in such a way that all the individual contributions to the EM field are periodic. The reason therefore lies in the usage of the differential method for the exposure/bleaching module. The periodicity guarantees that the ordinary differential equation system of (6) and the boundary matrices (10) are equal for all point sources. As a consequence the linear system (12) has to be assembled just once. The additional costs due to the partial coherence lie therefore only in the solution of (12) for multiple right hand sides. Hence, the periodic requirement is essential for a numerically efficient exposure/bleaching simulation.
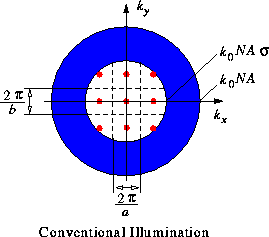
The spacing between the point sources
![]() is chosen to assure that the lateral wavevector components
is chosen to assure that the lateral wavevector components
![]() and
and
![]() of the waves incident onto the photomask equal an integer
multiple of the sampling frequencies
of the waves incident onto the photomask equal an integer
multiple of the sampling frequencies
![]() and
and
![]() in the Fourier domain.
This requirement is illustrated in the wavevector diagram of
Fig. 5.
in the Fourier domain.
This requirement is illustrated in the wavevector diagram of
Fig. 5.
The resulting image on top of the wafer due to one coherent point source can now be expressed by a superposition of discrete diffraction orders. Because of the periodicity of the EM field this superposition corresponds to a Fourier expansion and writes to
whereby
![]() stands vicariously for the two EM field vectors
stands vicariously for the two EM field vectors
![]() and
and
![]() .
The diffraction orders are homogeneous plane waves with wavevectors
.
The diffraction orders are homogeneous plane waves with wavevectors
![]() and amplitudes following from
the vector-valued diffraction theory
[7],
and amplitudes following from
the vector-valued diffraction theory
[7],
![]() is the actinic wavelength and
the time dependence of the EM field is a time-harmonic one,
i.e.,
is the actinic wavelength and
the time dependence of the EM field is a time-harmonic one,
i.e., ![]() and
and
![]() with angular frequency
with angular frequency
![]() .
.
In
(1)
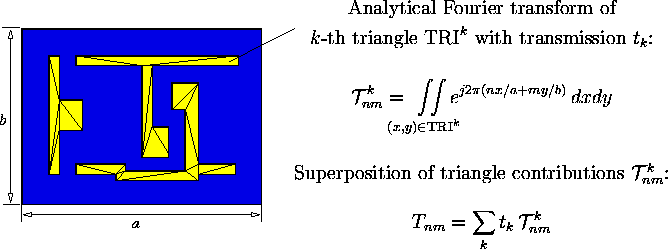
![]() stands for the Fourier coefficients of the mask transmission function.
As illustrated in
Fig. 6
they are computed by first triangulating the piecewise constant transmission
function and then
superposing weighted analytical Fourier transforms of the triangular patterns.
This semi-analyitcal algorithm has the great advantage of avoiding any errors due
to aliasing.
Aliasing would occur by conventional sampling of the transmission function
and application of the Fast Fourier Transform (FFT) algorithm, because
the mask transmittance is not a low pass function
[12].
stands for the Fourier coefficients of the mask transmission function.
As illustrated in
Fig. 6
they are computed by first triangulating the piecewise constant transmission
function and then
superposing weighted analytical Fourier transforms of the triangular patterns.
This semi-analyitcal algorithm has the great advantage of avoiding any errors due
to aliasing.
Aliasing would occur by conventional sampling of the transmission function
and application of the Fast Fourier Transform (FFT) algorithm, because
the mask transmittance is not a low pass function
[12].
The second term
![]() of
(1)
is the vector-valued counterpart to the pupil-function
of the scalar diffraction theory
[9]
and follows from
ray-tracing
[7]
[8]
trough the optical system
(cf. Fig. 3).
of
(1)
is the vector-valued counterpart to the pupil-function
of the scalar diffraction theory
[9]
and follows from
ray-tracing
[7]
[8]
trough the optical system
(cf. Fig. 3).
![]() is essentially a low-pass filter (no evanescent waves
can travel towards the wafer) and accounts
for the polarization state, defocus and higher order aberrations terms.
Hence, the vector-valued illumination spectrum
(1)
is band-limited and
the Fourier backward transform can be accomplished using FFT techiques
without any aliasing errors
[12].
As the Fourier forward transform, i.e., the Fourier coefficients
is essentially a low-pass filter (no evanescent waves
can travel towards the wafer) and accounts
for the polarization state, defocus and higher order aberrations terms.
Hence, the vector-valued illumination spectrum
(1)
is band-limited and
the Fourier backward transform can be accomplished using FFT techiques
without any aliasing errors
[12].
As the Fourier forward transform, i.e., the Fourier coefficients
![]() of the mask transmission function, is computed with the above
described semi-analyitcal algorithm,
the EM field is calculated aliasing free.
of the mask transmission function, is computed with the above
described semi-analyitcal algorithm,
the EM field is calculated aliasing free.
The aerial image itself is the light intensity
![]() incidenting on top of the wafer and is thus given by the
real part of the vertical component of the Poynting vector
of the EM field.
It is calculated by a weighted incoherent superposition of all
mutually independent terms and writes to
incidenting on top of the wafer and is thus given by the
real part of the vertical component of the Poynting vector
of the EM field.
It is calculated by a weighted incoherent superposition of all
mutually independent terms and writes to
![]()
whereby the asterisk denotes complex conjugation.
For a uniform bright source the weights
![]() are determined by the portion of the discretization rectangles
are determined by the portion of the discretization rectangles
![]() within the illumination cone
(cf. Fig. 5).
within the illumination cone
(cf. Fig. 5).
Simulation results of the aerial image module are shown in Fig. 1 and Fig. 11.