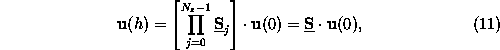H. Kirchauer and S. Selberherr: Three-Dimensional Photolithography Simulation


Next:
4 Development Simulation
Up:
3 Exposure/Bleaching Simulation
Previous:
3.1 Simulation Model
3.2 Numerical Solution of the Maxwell Equations
Our solution of the Maxwell equations corresponds to
the novel three-dimensional formulation of the differential method.
This method was originally developed for the simulation of diffraction gratings
[15]
and was later adapted for two-dimensional photolithography
simulation
[7].
The differential method itself requires a rectangular shaped
simulation domain
( )
with periodic boundary conditions in lateral direction.
Inside the simulation domain arbitrary inhomogeneous and
nonplanar regions can be simulated. Above
)
with periodic boundary conditions in lateral direction.
Inside the simulation domain arbitrary inhomogeneous and
nonplanar regions can be simulated. Above
 and below
and below
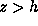 multiple planar homogeneous layers
form a stratified medium, that can be treated analytically and
is considered by the vertical boundary conditions.
A typical formation is shown in Fig. 8.
multiple planar homogeneous layers
form a stratified medium, that can be treated analytically and
is considered by the vertical boundary conditions.
A typical formation is shown in Fig. 8.
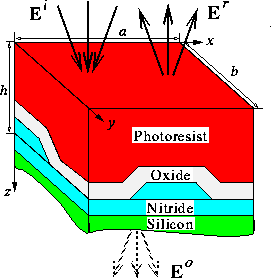
Figure 8:
In the given example the simulation domain
consists of the inhomogeneous photoresist,
the nonplanar Oxide and the nonplanar part of the Nitride.
Above 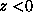 and below
and below
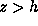 multiple planar homogeneous layers form a stratified medium.
multiple planar homogeneous layers form a stratified medium.
The strategy behind the differential method is briefly described as follows:
First, the dependency of the EM field on the lateral
x- and y-coordinates
is expressed by Fourier series. Insertion of these expansions into
the Maxwell equations transforms the partial
differential equations (PDEs) into a system of
ordinary differential equations (ODEs).
Once the boundary conditions (BCs) are determined and the ODE system
is solved, the obtained field coefficients
are transformed back to the spatial domain.
A schematic overview of the various steps involved in the
numerical algorithm is illustrated in
Fig. 9.

Figure 9:
Overview of the numerical algorithm.
A more detailed discussion of the
lateral discretization,
the
boundary conditions,
and the
vertical discretization
is presented in the following three items:
-
Lateral Discretization:
Due to the periodic nature of the
incident light
and the assumed lateral periodicity of the
simulation domain
the EM field as well as the permittivity
inside the simulation domain can be expressed by
Fourier series,
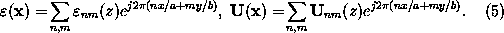
Here, it is most important to emphasize that the above
expansions are valid for all point sources 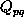 and time steps
and time steps 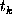 .
.
Insertion of
(5) into
(3)
transforms the PDEs into an infinite dimensional set of coupled ODEs
for the Fourier coefficients of the lateral field components, as
the vertical field components can be expressed analytically by the lateral
ones.
Next, the Fourier expansions of
(5)
are truncated. Thus, only coefficients
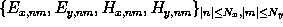 symmetrically centered around the vertical incident ray n=m=0
are related by the final ODE-system,
symmetrically centered around the vertical incident ray n=m=0
are related by the final ODE-system,
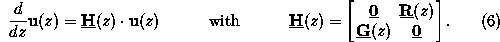
In the above matrix-vector notation the
complex-valued vector
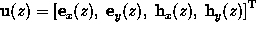 comprises the Fourier coefficients of the lateral field components,
e.g.
comprises the Fourier coefficients of the lateral field components,
e.g.
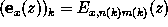 ,
and the elements
,
and the elements
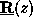 and
and
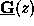 of the system matrix
of the system matrix
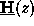 contain the Fourier coefficients of the permittivity
contain the Fourier coefficients of the permittivity
 .
Each of the e and h vectors has dimension
.
Each of the e and h vectors has dimension
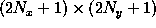 due to the symmetric truncation.
Therefore, the entire ODE system is of dimension
due to the symmetric truncation.
Therefore, the entire ODE system is of dimension
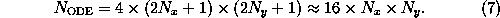
-
Boundary Conditions:
Above and below the simulation domain we have homogeneous planar layers
(cf. Fig. 8).
Inside one layer the EM field can be
expressed by a plane wave or Rayleigh expansion
[16].
The mathematical formulation is that of a Fourier series with
vertically known dependency of the coefficients.
Above the simulation domain
(
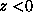 )
we have to consider incident and reflected waves,
)
we have to consider incident and reflected waves,
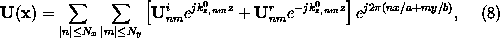
below
(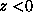 )
only outgoing waves occur disregarding multiple planar layers,
)
only outgoing waves occur disregarding multiple planar layers,
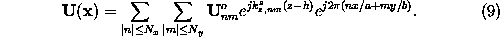
The extension to the general situation of a vertically
stratified medium is straight forward
[16]
and therefore skipped in this paper.
Matching the two Rayleigh expansions
(8)
and
(9)
with the field representation
(5),
valid inside the simulation domain,
and eliminating the unknown reflected and outgoing wave amplitudes,
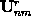 and
and
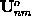 ,
respectively, yields exactly half of the BCs at the top
(z=0)
and at the bottom
(z=h)
of the simulation domain.
The incident amplitudes
,
respectively, yields exactly half of the BCs at the top
(z=0)
and at the bottom
(z=h)
of the simulation domain.
The incident amplitudes
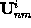 are of course involved
in the BCs as the excite the EM field inside the simulation domain.
They are the output of the illumination simulation and given by
(1).
This means that we have different excitation vectors
for each coherent point source
are of course involved
in the BCs as the excite the EM field inside the simulation domain.
They are the output of the illumination simulation and given by
(1).
This means that we have different excitation vectors
for each coherent point source
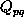 .
Using the above introduced vector notation we find
.
Using the above introduced vector notation we find

However, the two rectangular matrices
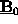 and
and
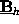 are independent of the specific
are independent of the specific
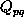 ,
whereas the excitation vector
,
whereas the excitation vector
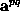 comprises the incoming wave amplitudes
comprises the incoming wave amplitudes
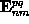 and
and
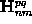 of one coherent point source contribution.
This means, that we have transformed the Maxwell equations
(3)
into a linear complex-valued two-point boundary value problem
(6) and
(10)
with multiple BCs.
of one coherent point source contribution.
This means, that we have transformed the Maxwell equations
(3)
into a linear complex-valued two-point boundary value problem
(6) and
(10)
with multiple BCs.
-
Vertical Discretization:
We adapted the memory saving ``shooting method''
[17]
as it allows a very efficient treatment of the
multiple right hand sides of the first BC in
(10).
The algorithm is based on the observation, that the system matrix
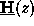 in
(6)
as well as the two boundary matrices
in
(6)
as well as the two boundary matrices
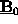 and
and
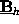 of
(10)
are independent of the chosen point source.
This property is a direct consequence of the special
source discretization procedure yielding a periodic incident field
as discussed below
Fig. 4.
of
(10)
are independent of the chosen point source.
This property is a direct consequence of the special
source discretization procedure yielding a periodic incident field
as discussed below
Fig. 4.
Exploiting this
situation, we first establish a relation between the two boundary
points z=0 and z=h, which
is accomplished by applying an explicit discretization scheme to
(6).
The obtained recursion formula
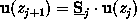 between two adjacent mesh points
is then successively evaluated,
between two adjacent mesh points
is then successively evaluated,
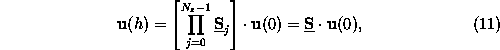
whereby
 is the number of vertical discretization points.
Combining this equation with the second BC of
(10)
yields
is the number of vertical discretization points.
Combining this equation with the second BC of
(10)
yields
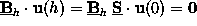 ,
which forms together with the first BC of
(10)
a linear algebraic system for the initial values
,
which forms together with the first BC of
(10)
a linear algebraic system for the initial values
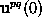 due to one excitation vector
due to one excitation vector
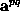 ,
,
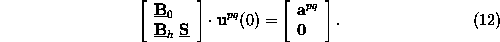
This linear system is solved by performing a LU decomposition, which
is an extremely efficient solution method for linear systems with
multiple right hand sides
[18].
Once the initial values
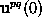 are found, the solution vector
are found, the solution vector
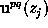 inside the simulation domain
is calculated by integrating the ODE system
(6).
As the elements of
inside the simulation domain
is calculated by integrating the ODE system
(6).
As the elements of
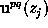 correspond to the
Fourier coefficients of the EM field, they have to be
transformed back to the spatial domain. Finally, the point source
contributions are incoherently superposed to
build up the absorbed light intensity within the photoresist, which is
needed in
(4)
for the exposure/bleaching model.
correspond to the
Fourier coefficients of the EM field, they have to be
transformed back to the spatial domain. Finally, the point source
contributions are incoherently superposed to
build up the absorbed light intensity within the photoresist, which is
needed in
(4)
for the exposure/bleaching model.
The proposed algorithm has the great advantage that the vertical mesh size
 does not influence the storage consumption
as the recursion matrices
does not influence the storage consumption
as the recursion matrices
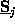 in
(11)
do not have to be stored individually.
The memory usage is therefore only determined by the rank
in
(11)
do not have to be stored individually.
The memory usage is therefore only determined by the rank
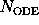 of the ODE system
(7)
and is of order
of the ODE system
(7)
and is of order
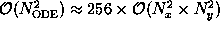 .
Typically 31 Fourier coefficients are needed for each lateral direction.
In this case
.
Typically 31 Fourier coefficients are needed for each lateral direction.
In this case
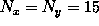 and the ODE system is of rank
and the ODE system is of rank
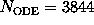 .
Assuming 16 Bytes for a double precision complex number, approximately
250 MB memory are required to store the system matrix.
For three-dimensional rigorous photolithography simulation
this storage consumption is in accordance with other frequency-domain
methods
(e.g., [6]),
and lies dramatically below time-domain methods
(e.g., [3]).
.
Assuming 16 Bytes for a double precision complex number, approximately
250 MB memory are required to store the system matrix.
For three-dimensional rigorous photolithography simulation
this storage consumption is in accordance with other frequency-domain
methods
(e.g., [6]),
and lies dramatically below time-domain methods
(e.g., [3]).
For the investigation of the numerical costs we have to bear in mind, that
the Maxwell equations
(3)
have to be solved for multiple time steps
(cf. Fig. 7).
The numerical costs for one time step
are mainly determined by the evaluation of the recursion
(11) and by the solution of
(12).
Both operations are of order
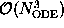 .
Hence, the total run-time grows for
.
Hence, the total run-time grows for
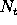 time steps and
time steps and
 vertical discretization points with
vertical discretization points with
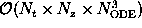 and is typically under a few hours on a DEC-600 workstation.
Finally it is worth mentioning, that the number of simulated
point sources does not significantly influence the simulation time,
which is an unique feature of the proposed discretization method.
and is typically under a few hours on a DEC-600 workstation.
Finally it is worth mentioning, that the number of simulated
point sources does not significantly influence the simulation time,
which is an unique feature of the proposed discretization method.


Next:
4 Development Simulation
Up:
3 Exposure/Bleaching Simulation
Previous:
3.1 Simulation Model
H. Kirchauer and S. Selberherr: Three-Dimensional Photolithography Simulation