Next: 6 Power Consumption Up: VLSI Performance Metric Based Previous: 4 Key Parameters and

5 Dynamic Inverter Model

The inverter delay t_d is determined by the drive current I_on, V_DD, the nonlinear capacitances of the intrinsic transistors, and the interconnect capacitances. The capacitances are modeled into a single load capacitance at the inverter output (cf. Fig. 3 and (2)).

**Figure 3:** Dynamic inverter model
$\begin{figure} \centerline{\epsfysize=3cm\epsfbox{invckt.eps} \hspace{6mm} \epsfysize=5cm\raisebox{6mm}{\rotate[r]{\epsfbox{invmod.eps}}}}\end{figure}$

The influence of the nonlinear capacitances can also be formulated as follows: For switching one transistor a total switching charge of

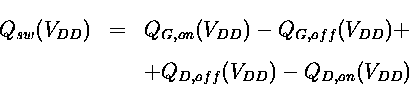$\begin{displaymath}\aatrue {\renewcommand {\arraystretch}{1.6} \begin{array}{r... ... &+Q_{D,off}(V_{DD})-Q_{D,on}(V_{DD}) \end{array} }\aafalse \end{displaymath}$

(1)

is transferred. The charges can be obtained as a function of V_DD from two transient simulations (3a, 3b) as shown in Fig. 4 [3]. The trajectory used to determine the charges (solid line) is different from the actual switching trajectory (dashed line), which is justified by the quasi-static model. The switching charge Q_sw covers automatically all parasitic capacitances of the simulated device structure.

**Figure 4:** Transient determination of the switching charge Q_sw
$\begin{figure} \centerline{\epsfysize=5.5cm\rotate[r]{\epsfbox{qsw-idea.eps}} \... ...\epsfysize=3.0cm\raisebox{3mm}{\rotate[r]{\epsfbox{qsw-sim-x.eps}}}}\end{figure}$

An effective load capacitance C_L including interconnects is then determined as

$\begin{displaymath} C_L= \frac{Q_{sw}}{V_{DD}} k_2 + c_ML_M \end{displaymath}$

(2)

and the loaded-inverter delay is estimated as

$\begin{displaymath} t_d= \frac{V_{DD}C_L}{k_1 (I_{on}- I_{off})} \cdot k_3 \end{displaymath}$

(3)

Assuming an inverter chain the maximum clock frequency becomes then

$\begin{displaymath} f_{c,max}= \frac {1}{t_dld} \end{displaymath}$

(4)

The factors k₁ and k₂ are used to scale the data of one device to obtain the delay of a CMOS inverter. They account for the effective average drive current ((I_on,n-I_off,n)+(I_on,p-I_off,p))/2 = k₁ (I_on-I_off) and for the effective total capacitance (Q_sw,n+Q_sw,p)/V_DD= k₂ Q_sw/V_DD. Typically, for a CMOS inverter with minimum-size transistors these factors are k₁ = 0.75 and k₂ > 2 for NMOS data.

The empirical correction factor k₃ is typically < 1 and accounts for the fact that in a circuit the output nodes start to switch before the input pulse edge is complete. k₃ was determined from device-level simulations of a ring oscillator with MINIMOS-NT [5] as follows: setting k₁=((I_on,n-I_off,n)+(I_on,p-I_off,p))/2(I_on,n-I_off,n) and k2=(Q_sw,n+Q_sw,p)/Q_sw,n, yields k₃=t_d,osc/(k₂Q_sw/k₁(I_on,n-I_off,n)), where t_d,osc is the reference delay time determined from the ring oscillator. Using the devices of Section 8 k₃ was found to be 0.63. The value of k₃ does not change much with technology. Evaluating (3) with the same value of k₃ for a completely different technology (an ultra-low-power technology with Vdd=0.2V [6]) using both NMOS and PMOS data gave an error of -22%.

Although (3) and (4) are generally not very accurate, they reflect the various tendencies very closely and are therefore well-suited for optimization purposes. Furthermore, the device characterization method, which is specific to this approach, can be combined with a more detailed system model (cf. [7]) to account for the effect of the particular circuit design style and metalization scheme.

Next: 6 Power Consumption Up: VLSI Performance Metric Based Previous: 4 Key Parameters and

G. Schrom, V. De, and S. Selberherr: VLSI Performance Metric Based on Minimum TCAD Simulations