4.2.2 Examples

In the following two examples are presented. In the first the well-known model equation for diffusion

$$\frac{\partial{C}}{\partial{t}}=\nabla\cdot D\nabla{C}$$

with homogeneous Neumann boundary conditions (mass conservation, no flux to/from the outside), a backward Euler time discretization and no lumping is simulated. As initial profile a spherical Gaussian distribution with a high gradient was chosen. Note that the pictures are drawn in black and white in order to better illustrate the occurrence of the negative dopant concentrations.

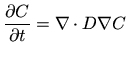
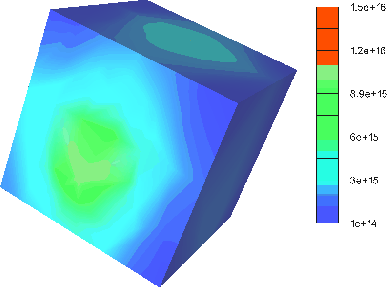
The first example (Fig. 4.10 and Fig. 4.11) depicts a cube with $650$ elements which was refined to $\approx 3100$ elements during the simulation. Both figures depict the result after the same time. Fig. 4.10 illustrates the unrefined case. Negative concentrations emerged and the symmetry of the Gaussian profile is violated. Fig. 4.11 shows the result of the simulation with the refinement algorithm turned on. Negative concentrations are not visible.

The second example demonstrates the locality of the implemented refinement algorithm. Fig. 4.12 displays a part of the schematic transistor cell of Fig. 4.4. The aim of this example was to locally refine the gate region. To achieve this local refinement all edges within a rectangular region around the gate were marked for refinement. Fig. 4.13 depicts the final mesh after the refinement was performed. The locality of the refinement algorithm is clearly visible.

Figure 4.10: Original mesh - negative concentrations emerge during the simulation. The symmetry of the spherical Gaussian profile is violated.

Figure 4.11: Adaptively refined mesh - negative concentrations have not occurred. The symmetry of the spherical Gaussian profile is reproduced.

Figure 4.12: Original coarse mesh.

Figure 4.13: Final mesh. Refinement is restricted to the gate region.

2003-03-27