


Next: 5.3 Device Simulation
Up: 5. Results
Previous: 5.1 Low-Field Mobility Modeling
Subsections
5.2 High-Field Electron Transport in Strained Si
In this section, the electron high-field transport in Si under biaxial and
uniaxial stress conditions is studied and some peculiarities of the
velocity-field characteristics in strained Si are presented. The velocity-field
characteristics have been obtained by full-band Monte Carlo simulations using
VMC [IuE06] and compared with the analytical model developed in
Section 4.6. Results of full-band Monte Carlo simulations have been
calibrated with the existing theoretical and experimental data.
It was discussed in Section 5.1 that the enhancement of the bulk
low-field electron mobility saturates at around 1.7 [Dhar05b]. In order
to maintain the desired mobility enhancement, the g-type and f-type coupling
constants had to be adjusted to the values stated in
Table 5.1. In addition, it was required to adjust the
acoustic deformation potential from its original value of 8.9
eV [Jungemann03a] for analytical band Monte Carlo to 8.5 eV for full-band
Monte Carlo simulation. The effect of impact ionization was neglected for the
field regime investigated.
Fig. 5.11 presents the velocity-field characteristics for
unstrained and strained Si for different field directions as obtained from
Monte Carlo simulations. Also displayed are the results from
Bufler [Bufler97], Canali [Canali71], Smith [Smith80],
Fischer [Fischer99], and Ismail [Ismail93]. The simulation results
agree well with measured data from Smith for the [111] field direction and with
Canali for the [100] field direction for the unstrained case and with
Jungemann [Jungemann03a], Bufler, and Ismail for the strained case.
Figure 5.11:
Comparison of electron velocity versus field characteristics in
unstrained and strained ( ) Si on Si
) Si on Si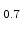 Ge
Ge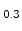 for [100] and
[111] field directions.
for [100] and
[111] field directions.
Fig. 5.12 depicts the velocity-field characteristics as
obtained from Monte Carlo simulations for biaxially strained Si grown on a
relaxed SiGe substrate for different Ge content and field along the in-plane
([100]) and out-of-plane ([001]) direction, respectively. The total velocity
increases with strain for a field along the [100] direction and it decreases
for a field along the [001] direction. For the in-plane electric field ([100])
the electron velocity shows a region of small negative differential mobility.
The velocity-field characteristics for field along the [001] direction exhibit
an untypical form for high strain levels. This phenomenon can be explained as
follows. For field along [001] direction the 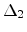 -valleys are lowered in
energy with increasing strain and have the longitudinal mass in the field
direction. These valleys are located at a scaled distance of 0.85 and 1.15 from
the center of the first Brillouin zone and are separated by an energy barrier
of 129 meV at the X-point (Fig. 5.13). The average velocity in
the left and right valley and also the average of these velocities are shown
in Fig. 5.14. For low-fields, electrons in both valleys
are slightly displaced with respect to the valley minima. This results in the
initial velocity increase for both valleys shown in
Fig. 5.14. However, as the field increases, electrons in
both valleys gain energy, and electrons from one valley can surpass the energy
barrier and drift to the valley in the next Brillouin zone. As sketched in
Fig. 5.13, there are more electrons populating the right side
of the double valley than the left side, giving rise to a slight increase in
average velocity. If only the left valley is considered, there are more
electrons populating the left edge of the single valley resulting in a negative
valley velocity, as shown in Fig. 5.14.
-valleys are lowered in
energy with increasing strain and have the longitudinal mass in the field
direction. These valleys are located at a scaled distance of 0.85 and 1.15 from
the center of the first Brillouin zone and are separated by an energy barrier
of 129 meV at the X-point (Fig. 5.13). The average velocity in
the left and right valley and also the average of these velocities are shown
in Fig. 5.14. For low-fields, electrons in both valleys
are slightly displaced with respect to the valley minima. This results in the
initial velocity increase for both valleys shown in
Fig. 5.14. However, as the field increases, electrons in
both valleys gain energy, and electrons from one valley can surpass the energy
barrier and drift to the valley in the next Brillouin zone. As sketched in
Fig. 5.13, there are more electrons populating the right side
of the double valley than the left side, giving rise to a slight increase in
average velocity. If only the left valley is considered, there are more
electrons populating the left edge of the single valley resulting in a negative
valley velocity, as shown in Fig. 5.14.
Figure 5.12:
Electron velocity in strained Si on SiGe with Ge content as a
parameter for field along the [100] and [001]
directions.
Figure 5.13:
Asymmetric electron populations of the double valley close to the
equilibrium state (top) and at high-field (bottom). Solid circles indicate
electrons with positive group velocity (right side of each valley). Open
circles refer to electrons with negative group velocity (left side of each
valley).
Figure 5.14:
Velocity versus field for the left valley and right valley together
with the average valley velocity, computed by full-band Monte Carlo
simulations.
5.2.1 Analytical High Field Velocity Model
For the empirical model, the parameters in (4.108) to (4.112) have been
obtained using the optimization framework of MATLAB [MATLAB04]. A
multidimensional unconstrained nonlinear minimization (Nelder-Mead) technique
was adopted for obtaining the parameter set. The optimized values of the
parameters for these field directions are listed in Tables 5.2.1
to 5.2.1. It should be noted that the optimization technique is
sensitive to the initial conditions of the parameters and thus a small
variation in the initial conditions can result in a slightly varied parameter
set.
Fig. 5.15a shows the 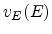 characteristics for a 1GPa stress
along [001] and the field along the [100] and [001] directions. Application of
uniaxial compressive stress enhances the velocity along the [100] direction in
the same way as biaxial tensile strain does. Conversely, applying uniaxial
tensile stress results in an enhanced velocity along the [001] direction. For
the perpendicular velocity the fitting of the parameters in (4.114) is
performed such that the error in
characteristics for a 1GPa stress
along [001] and the field along the [100] and [001] directions. Application of
uniaxial compressive stress enhances the velocity along the [100] direction in
the same way as biaxial tensile strain does. Conversely, applying uniaxial
tensile stress results in an enhanced velocity along the [001] direction. For
the perpendicular velocity the fitting of the parameters in (4.114) is
performed such that the error in 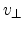 is minimized. The values of the
other parameters for the field directions [101] and [11
is minimized. The values of the
other parameters for the field directions [101] and [11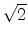 ] are listed
in Table 5.2.1. Fig. 5.15b shows the perpendicular
electron velocity
] are listed
in Table 5.2.1. Fig. 5.15b shows the perpendicular
electron velocity
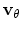 for field along the [101] direction for
increasing stress level as obtained from Monte Carlo simulations. The component
for field along the [101] direction for
increasing stress level as obtained from Monte Carlo simulations. The component
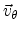 , although small for low stress levels, has a significant
magnitude for intermediate field regimes and can result in a total velocity
different from the parallel velocity.
, although small for low stress levels, has a significant
magnitude for intermediate field regimes and can result in a total velocity
different from the parallel velocity.
![\includegraphics[width=2.8in]{figures/rot_2e100_e001_vpar.ps}](img914.png)
![\includegraphics[width=2.8in]{figures/rot_Vprp.ps}](img915.png)

Figure 5.15:
(a) Parallel electron velocity component versus field for Si under
uniaxial stress (1GPa) along [001] and field along [100] and [001],
respectively. (b) Perpendicular velocity versus field for Si under increasing
uniaxial stress along [001] and field along [101].
![\includegraphics[width=2.8in]{figures/rot_VelvsE_all_e111414_m1GPa.ps}](img916.png)
![\includegraphics[width=2.8in]{figures/rot_Vel_all_interpolate_e111.ps}](img917.png)

Figure 5.16:
(a) Parallel (par) and perpendicular (prp) velocity components and
total (tot) velocity versus field for Si under 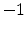 GPa uniaxial stress along
[001] and field along [11
GPa uniaxial stress along
[001] and field along [11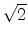 ]. (b) Interpolated parallel (par),
perpendicular (prp) velocity and the total (tot) velocity versus field for Si
under 3GPa uniaxial stress along [001] and field along [111].
]. (b) Interpolated parallel (par),
perpendicular (prp) velocity and the total (tot) velocity versus field for Si
under 3GPa uniaxial stress along [001] and field along [111].
It was found that interpolation of the quantities
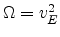 and
and
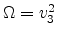 gives good agreement to the Monte Carlo data.
Fig. 5.16a shows a comparison of the velocity components and
total velocity for
gives good agreement to the Monte Carlo data.
Fig. 5.16a shows a comparison of the velocity components and
total velocity for  GPa stress for field along the [11
GPa stress for field along the [11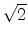 ]
direction, as obtained from Monte Carlo simulations and the analytical model. The
results from the model for the sample field direction chosen are in good
agreement with the Monte Carlo data and demonstrate the validity of the model.
]
direction, as obtained from Monte Carlo simulations and the analytical model. The
results from the model for the sample field direction chosen are in good
agreement with the Monte Carlo data and demonstrate the validity of the model.
Fig. 5.16b shows a comparison of the velocity components and the
total velocity as obtained from the interpolation and Monte Carlo simulations for field
along the [111] direction for uniaxial tensile stressed Si. In this case the
perpendicular velocity is negative.



Next: 5.3 Device Simulation
Up: 5. Results
Previous: 5.1 Low-Field Mobility Modeling
S. Dhar: Analytical Mobility Modeling for Strained Silicon-Based Devices
![\includegraphics[width=3in]{figures/rot_Uns-Str3.ps}](img852.png)
![\includegraphics[width=3in]{figures/rot_Uns-Str3.ps}](img852.png)
![]() -valleys are lowered in
energy with increasing strain and have the longitudinal mass in the field
direction. These valleys are located at a scaled distance of 0.85 and 1.15 from
the center of the first Brillouin zone and are separated by an energy barrier
of 129 meV at the X-point (Fig. 5.13). The average velocity in
the left and right valley and also the average of these velocities are shown
in Fig. 5.14. For low-fields, electrons in both valleys
are slightly displaced with respect to the valley minima. This results in the
initial velocity increase for both valleys shown in
Fig. 5.14. However, as the field increases, electrons in
both valleys gain energy, and electrons from one valley can surpass the energy
barrier and drift to the valley in the next Brillouin zone. As sketched in
Fig. 5.13, there are more electrons populating the right side
of the double valley than the left side, giving rise to a slight increase in
average velocity. If only the left valley is considered, there are more
electrons populating the left edge of the single valley resulting in a negative
valley velocity, as shown in Fig. 5.14.
-valleys are lowered in
energy with increasing strain and have the longitudinal mass in the field
direction. These valleys are located at a scaled distance of 0.85 and 1.15 from
the center of the first Brillouin zone and are separated by an energy barrier
of 129 meV at the X-point (Fig. 5.13). The average velocity in
the left and right valley and also the average of these velocities are shown
in Fig. 5.14. For low-fields, electrons in both valleys
are slightly displaced with respect to the valley minima. This results in the
initial velocity increase for both valleys shown in
Fig. 5.14. However, as the field increases, electrons in
both valleys gain energy, and electrons from one valley can surpass the energy
barrier and drift to the valley in the next Brillouin zone. As sketched in
Fig. 5.13, there are more electrons populating the right side
of the double valley than the left side, giving rise to a slight increase in
average velocity. If only the left valley is considered, there are more
electrons populating the left edge of the single valley resulting in a negative
valley velocity, as shown in Fig. 5.14.
![\includegraphics[width=3in]{figures/rot_2VelvsE_e100_e001.ps}](img853.png)
![\includegraphics[width=3in, angle=-0]{figures/repopulation5.eps}](img854.png)
![\includegraphics[width=3in]{figures/rot_valley_velocity.ps}](img855.png)
![\includegraphics[width=2.8in]{figures/rot_2e100_e001_vpar.ps}](img914.png)
![\includegraphics[width=2.8in]{figures/rot_Vprp.ps}](img915.png)
![]()
![\includegraphics[width=2.8in]{figures/rot_VelvsE_all_e111414_m1GPa.ps}](img916.png)
![\includegraphics[width=2.8in]{figures/rot_Vel_all_interpolate_e111.ps}](img917.png)
![]()