


Next: 4.7 The Onion Model
Up: 4. Mobility Modeling
Previous: 4.5 Inversion Layer Mobility
Subsections
4.6 High-Field Mobility
Figure 4.8:
Velocity saturation in Si.
With an increase in the applied lateral field, carriers gain energies above the
ambient thermal energy and are able to transfer energy to the lattice by
optical phonon emission. This effect leads to a saturation of the carrier
velocity as shown in Fig. 4.8. To account for this velocity
saturation, the mobility has to be reduced accordingly. Popular models
including this basic feature are the Caughey and Thomas
expression [Caughey67],
![$\displaystyle \mu = \frac{\mu_0}{\left[1 + \left(\displaystyle \frac{\mu_0 E}{v_s}\right)^\beta \right]^{1/\beta} }$](img670.png) |
(4.104) |
and its modification [IuE04],
![$\displaystyle \displaystyle \mu_{E} = \frac{2 \mu_0 }{1+\left[1+\left(\displaystyle \frac{2\mu_0 E }{ \displaystyle v_{s} }\right)^{\beta}\right]^{1/\beta} }.$](img671.png) |
(4.105) |
Here 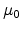 denotes the low field mobility and
denotes the low field mobility and 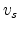 the saturation
velocity. The parameter
the saturation
velocity. The parameter 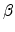 influences the transition from low to high
fields. Although (4.104) and (4.105) are applicable for a
uniform field, they can be used for device simulations where the fields are
non-uniform by making an appropriate choice of the lateral field. Different
alternatives are available such as (a) the magnitude of the gradient of the
quasi-fermi potential, (b) the component of electric field in the direction of
current flow, and (c) the component of electric field parallel to the
interface. Any of the definitions can be considered for device simulation
purposes.
influences the transition from low to high
fields. Although (4.104) and (4.105) are applicable for a
uniform field, they can be used for device simulations where the fields are
non-uniform by making an appropriate choice of the lateral field. Different
alternatives are available such as (a) the magnitude of the gradient of the
quasi-fermi potential, (b) the component of electric field in the direction of
current flow, and (c) the component of electric field parallel to the
interface. Any of the definitions can be considered for device simulation
purposes.
4.6.1 Analytical High Field Velocity Model
In general, the high field mobility is modeled differently for the
drift-diffusion and the hydrodynamic transport model. In the former case
mobility is modeled as a function of the driving force, whereas in the latter
case a dependence on the carrier temperature is usually assumed. To describe
nonlocal transport effects occurring in aggressively scaled devices a mobility
model for the hydrodynamic framework would be desirable. Such a model could
include a three-valley band structure and deal with arbitrary strain
conditions. It would capture the essential physics of multi-valley transport
under a spatially rapidly varying electric field profile. However, one problem
is complexity. A nonlinear system of nine unknowns, namely the valley
populations, valley velocities and valley temperatures, has to be solved
numerically. The strain and carrier temperature dependence for each valley would require
careful modeling in order to obtain realistic carrier temperatures and,
consequently, realistic valley population. In the past,
multi-valley transport models have also been devised for compound
semiconductors [Hänsch91]. As a matter of fact, it seems that such
multi-valley transport models with separate carrier gases for each valley have
never found application in commercial or academic device simulators.
To find a trade-off between physical rigor and an acceptable level of model
complexity we abstained from the multi-valley approach and pursued a more
empirical approach, where analytical expressions for the velocity-field
characteristics are directly fitted to bulk Monte Carlo data. The model is
restricted to such strain conditions where only one pair of X-valleys is
shifted and four valleys remain degenerate. These conditions include biaxial
stress and uniaxial stress applied along the  100
100 axes of
Si. Another condition resulting in a separation of the
axes of
Si. Another condition resulting in a separation of the 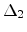 and
and
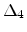 valleys is uniaxial stress in the [110]
direction. Equation (3.42) shows that the valley splitting depends only
on the diagonal elements of the strain tensor. The proposed mobility model is
thus applicable, if two diagonal elements are equal,
valleys is uniaxial stress in the [110]
direction. Equation (3.42) shows that the valley splitting depends only
on the diagonal elements of the strain tensor. The proposed mobility model is
thus applicable, if two diagonal elements are equal,
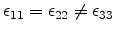 .
.
To develop a clear understanding of the model, we have to consider three
different coordinate systems.
- The principal coordinate system has to be oriented such that the unit
vectors
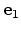 ,
,
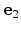 , and
, and
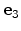 correspond to the [100],
[010], and [001] crystallographic directions, respectively. In this system
the
correspond to the [100],
[010], and [001] crystallographic directions, respectively. In this system
the 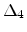 -valleys are aligned along the [100] and [010] directions,
whereas the
-valleys are aligned along the [100] and [010] directions,
whereas the 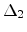 - valleys are aligned along the [001] direction.
- valleys are aligned along the [001] direction.
- The unit vectors
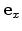 ,
,
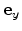 , and
, and
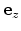 constitute the
device coordinate system. In this system the device geometry is defined. For
performing device simulations it is essential to transform all transport
parameters into this coordinate system.
constitute the
device coordinate system. In this system the device geometry is defined. For
performing device simulations it is essential to transform all transport
parameters into this coordinate system.
- A polar coordinate system is employed, comprising a unit vector along the
field direction,
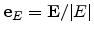 , and two orthogonal vectors
, and two orthogonal vectors
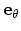 and
and
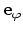 . The polar axis is aligned with the
[001] direction. In terms of the polar angle
. The polar axis is aligned with the
[001] direction. In terms of the polar angle 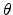 and the in-plane (azimuth) angle
and the in-plane (azimuth) angle
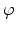 , the unit vectors are defined as follows.
, the unit vectors are defined as follows.
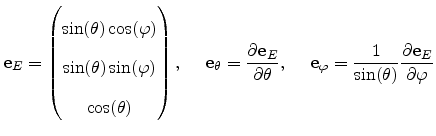 |
(4.106) |
Although (4.105) can describe the high field behavior in unstrained
Si, it cannot produce the peculiarities of the velocity field relation in
the strained case. Here the following expression has been suggested which can handle all types of
velocity-field characteristics resulting from the Monte Carlo simulations
performed [Dhar05a,Dhar06].
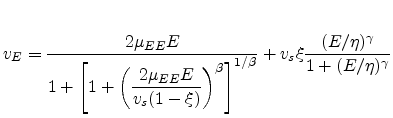 |
(4.107) |
Here 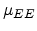 denotes the low-field mobility in the field direction, obtained
by projection of the low-field mobility tensor as
denotes the low-field mobility in the field direction, obtained
by projection of the low-field mobility tensor as
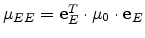 . The last term incorporated in (4.107) models the
velocity kink shown in Fig. 5.12. The relevance of the
parameter
. The last term incorporated in (4.107) models the
velocity kink shown in Fig. 5.12. The relevance of the
parameter 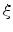 is twofold: It accounts for the velocity plateau occurring
approximately at
is twofold: It accounts for the velocity plateau occurring
approximately at
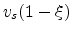 and also signifies the small negative
differential mobility occurring in strained Si for higher strain levels. The
parameters
and also signifies the small negative
differential mobility occurring in strained Si for higher strain levels. The
parameters 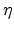 and
and 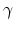 are fitting parameters.
are fitting parameters.
All parameters depend on the strain-induced valley splitting,
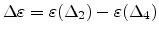 . The following
empirical expressions were assumed.
. The following
empirical expressions were assumed.
For all parameters except 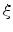 , a linear dependence was found to be
sufficient. The parameter
, a linear dependence was found to be
sufficient. The parameter 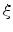 was modeled by the rational expression
in (4.112). The parameters
was modeled by the rational expression
in (4.112). The parameters 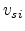 ,
, 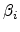 ,
, 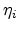 ,
,
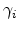 ,
,
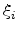 where
where 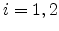 , are constants for a particular field direction. We
have chosen the three high symmetry directions [100], [110], and [001] and two
additional directions [101] and [11
, are constants for a particular field direction. We
have chosen the three high symmetry directions [100], [110], and [001] and two
additional directions [101] and [11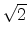 ]. These five sample directions
form a spherical triangle on a unit sphere as shown in Fig. 4.9.
]. These five sample directions
form a spherical triangle on a unit sphere as shown in Fig. 4.9.
Figure 4.9:
Spherical triangle with the five field directions
chosen.
For the cases where the field is not oriented along a high symmetry direction,
it is observed that an electron velocity component perpendicular to the field
direction develops. The component
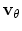 , although small for low stress levels, has a
significant magnitude for intermediate field regimes and results in a total
velocity different from the parallel velocity. For symmetry reasons, the
velocity component in the
, although small for low stress levels, has a
significant magnitude for intermediate field regimes and results in a total
velocity different from the parallel velocity. For symmetry reasons, the
velocity component in the
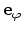 direction vanishes for all five
sample directions.
direction vanishes for all five
sample directions.
The perpendicular velocity component vanishes for fields along the [100], [110]
and [001] directions. For the field directions [101] and [11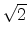 ], the
normal velocity can be expressed in terms of
], the
normal velocity can be expressed in terms of 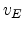 and
and 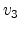 .
.
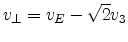 |
(4.113) |
After fitting 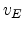 , the component
, the component 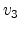 is fitted using an expression similar
to (4.107)
is fitted using an expression similar
to (4.107)
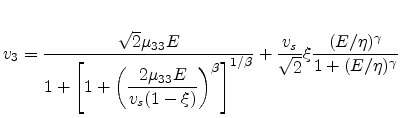 |
(4.114) |
To ensure the correct low-field behavior,
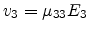 , the magnitude of
the electric field
, the magnitude of
the electric field 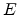 in the first term in (4.107) has to be replaced by
in the first term in (4.107) has to be replaced by
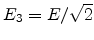 to obtain (4.114). The correct high-field limit is
introduced by replacing
to obtain (4.114). The correct high-field limit is
introduced by replacing 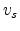 in (4.107) by
in (4.107) by
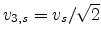 .
.
The total electron velocity vector for a fixed field direction is obtained by
addition of the two components.
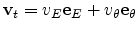 |
(4.115) |
where
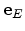 and
and
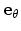 are the unit vectors parallel and
perpendicular to the field direction.
are the unit vectors parallel and
perpendicular to the field direction.
The velocity-field characteristics can be extended to other field directions
using a spherical harmonics interpolation.
![$\displaystyle \Omega(\theta,\varphi) = \sum_{l=0}^{\infty}\sum_{m=0}^{l}a_{lm}P_l^m[\cos(\theta)]\cos(m\varphi)$](img720.png) |
(4.116) |
Here, 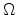 is the function to be interpolated,
is the function to be interpolated, 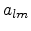 denote the expansion
coefficients and
denote the expansion
coefficients and 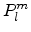 are the associated Legendre polynomials. From the
symmetry properties
are the associated Legendre polynomials. From the
symmetry properties
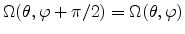 and
and
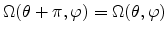 it follows that
it follows that  must be
even and
must be
even and 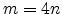 . Truncating (4.116) after the 4
. Truncating (4.116) after the 4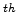 order
yields
order
yields
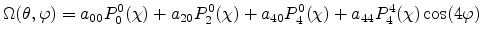 |
(4.117) |
where
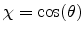 . Evaluating (4.117) for the field
directions [100], [110], [001], [101] and [11
. Evaluating (4.117) for the field
directions [100], [110], [001], [101] and [11 ] gives
] gives
To determine the four coefficients from the overdetermined
system (4.118) to (4.122), we solve (4.118) to
(4.120) exactly and minimize the error in (4.121) and
(4.122), as shown in Appendix B.
4.6.5 Simplification to Two-Dimensional Simulation Domains
For two-dimensional simulation domains a simpler interpolation method can be
used. In the following we consider the case that
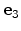 lies in the
simulation domain, such that
lies in the
simulation domain, such that 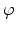 is fixed and only the variation of
is fixed and only the variation of
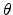 has to be considered. An alternative case would be a uniaxial stress
orthogonal to the simulation domain, for example, in the width direction of a
MOSFET. Then
has to be considered. An alternative case would be a uniaxial stress
orthogonal to the simulation domain, for example, in the width direction of a
MOSFET. Then
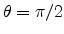 and
and 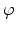 varies.
varies.
In the first case the quantity 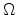 can be interpolated using the following
polynomial.
can be interpolated using the following
polynomial.
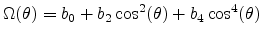 |
(4.127) |
Considering the special case of transport in the ( ) plane (
) plane (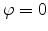 ),
we can write the equation system
),
we can write the equation system
which gives the coefficients
Similarly, for transport in a (
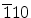 ) plane
(
) plane
(
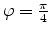 ), we have
), we have
giving
The present model has been derived for a uniform electric field
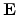 . To
apply it in a drift diffusion based device simulator, the electric field in the
model has to be replaced by an appropriately defined driving force
. To
apply it in a drift diffusion based device simulator, the electric field in the
model has to be replaced by an appropriately defined driving force
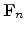 . Typical definitions of the driving force employed in practical
devices simulators are the electric field component along the current density
vector or the gradient of the quasi Fermi level.
. Typical definitions of the driving force employed in practical
devices simulators are the electric field component along the current density
vector or the gradient of the quasi Fermi level.
For the two-dimensional cases described in Section 4.6.5, only one
angle has to be determined. With the constant, two-dimensional vector
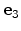 denoting the [001] direction, one obtains for the polar angle
denoting the [001] direction, one obtains for the polar angle
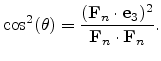 |
(4.138) |
The involved vectors are two-dimensional and specified in the device coordinate
system.
The task of finding a tensor
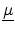 that relates two given vectors
that relates two given vectors
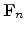 and
and
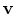 by
by
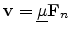 has no unique solution. In
two dimensions, this vector equation denotes two scalar equations, whereas the
2 by 2 matrix
has no unique solution. In
two dimensions, this vector equation denotes two scalar equations, whereas the
2 by 2 matrix
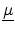 has four unknown elements. The straightforward
assumption of a diagonal matrix with diagonal elements
has four unknown elements. The straightforward
assumption of a diagonal matrix with diagonal elements
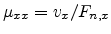 and
and
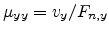 cannot be made, because this definition
becomes singular whenever the driving force vector is parallel to the
cannot be made, because this definition
becomes singular whenever the driving force vector is parallel to the 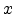 or
or
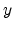 axis.
axis.
To solve this problem one can probe the velocity vector for a second driving
force vector. Using Cartesian coordinates, a vector orthogonal to
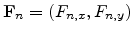 can be easily found as
can be easily found as
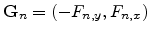 . The four matrix elements can now be uniquely determined from the
following two vector equations.
. The four matrix elements can now be uniquely determined from the
following two vector equations.
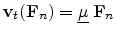 |
(4.139) |
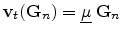 |
(4.140) |
Implementation of a full tensorial mobility model in two dimensions
would require the following quantities. We consider some edge 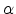 of an
unstructured mesh, connecting the nodes
of an
unstructured mesh, connecting the nodes 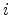 and
and 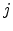 . The unit vector along this
edge is given by
. The unit vector along this
edge is given by
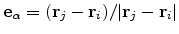 . A vector
. A vector
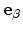 orthogonal to
orthogonal to
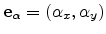 can be defined as
can be defined as
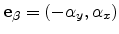 .
The box integration method requires the projection of the current density onto
the edge,
.
The box integration method requires the projection of the current density onto
the edge,
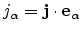 . For a mobility tensor
with non-zero off-diagonal elements this current component becomes
. For a mobility tensor
with non-zero off-diagonal elements this current component becomes
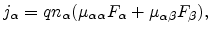 |
(4.141) |
where 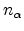 denotes the carrier concentration at the mid point edge
denotes the carrier concentration at the mid point edge
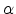 . This equation states that the current component along the edge is
driven not only by the driving force component along the edge,
. This equation states that the current component along the edge is
driven not only by the driving force component along the edge, 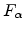 , but
also by the perpendicular component
, but
also by the perpendicular component 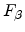 . The Scharfetter-Gummel
scheme [Scharfetter69] gives a discrete representation of the component
. The Scharfetter-Gummel
scheme [Scharfetter69] gives a discrete representation of the component
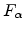 as a function of the variables at nodes
as a function of the variables at nodes 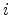 and
and 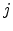 . The
perpendicular component
. The
perpendicular component 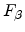 , however, cannot be determined from the
variables at the two nodes. It can only be estimated by some kind of
interpolation of the parallel components at neighboring edges. One possible
extension of the Scharfetter-Gummel discretization has been proposed
in [Egley93].
, however, cannot be determined from the
variables at the two nodes. It can only be estimated by some kind of
interpolation of the parallel components at neighboring edges. One possible
extension of the Scharfetter-Gummel discretization has been proposed
in [Egley93].
The high-field velocity model presented has been derived for bulk Si. The model
can consistently be used with the drift-diffusion transport model whenever the
spatial variations of the potential are sufficiently smooth. However, even
nowadays where gate lengths are in the deca-nanometer regime, drift-diffusion
based simulations are still widely used to estimate transistor performance,
despite the fact that this model cannot capture the strong non-local transport
effects. The latter are usually accommodated by changing parameters, in
particular by considerably increasing the saturation velocity. Also the
high-field velocity model presented cannot include non-local effects, as it is
based on populations of the band minima being functions of the local electric
field. One should be aware that extending the local drift-diffusion equation
with a local high-field velocity model cannot extend the limitation with
respect to strongly non-local transport occurring in relevant technologies.
Up-scaling the velocity by some technology-dependent parameter may still add
some physics to the model, as a rough estimate of the direction-dependence of
high-field transport.



Next: 4.7 The Onion Model
Up: 4. Mobility Modeling
Previous: 4.5 Inversion Layer Mobility
S. Dhar: Analytical Mobility Modeling for Strained Silicon-Based Devices
![\includegraphics[width=2.5in,angle=0]{figures/VdvsEcurve.eps}](img669.png)
![]() 100
100![]() axes of
Si. Another condition resulting in a separation of the
axes of
Si. Another condition resulting in a separation of the ![]() and
and
![]() valleys is uniaxial stress in the [110]
direction. Equation (3.42) shows that the valley splitting depends only
on the diagonal elements of the strain tensor. The proposed mobility model is
thus applicable, if two diagonal elements are equal,
valleys is uniaxial stress in the [110]
direction. Equation (3.42) shows that the valley splitting depends only
on the diagonal elements of the strain tensor. The proposed mobility model is
thus applicable, if two diagonal elements are equal,
![]() .
.
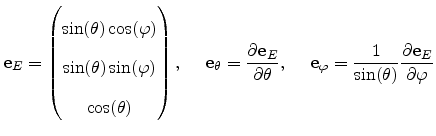
![]() denotes the low-field mobility in the field direction, obtained
by projection of the low-field mobility tensor as
denotes the low-field mobility in the field direction, obtained
by projection of the low-field mobility tensor as
![]() . The last term incorporated in (4.107) models the
velocity kink shown in Fig. 5.12. The relevance of the
parameter
. The last term incorporated in (4.107) models the
velocity kink shown in Fig. 5.12. The relevance of the
parameter ![]() is twofold: It accounts for the velocity plateau occurring
approximately at
is twofold: It accounts for the velocity plateau occurring
approximately at
![]() and also signifies the small negative
differential mobility occurring in strained Si for higher strain levels. The
parameters
and also signifies the small negative
differential mobility occurring in strained Si for higher strain levels. The
parameters ![]() and
and ![]() are fitting parameters.
are fitting parameters.
![]() . The following
empirical expressions were assumed.
. The following
empirical expressions were assumed.
![]() ], the
normal velocity can be expressed in terms of
], the
normal velocity can be expressed in terms of ![]() and
and ![]() .
.
![]() can be interpolated using the following
polynomial.
can be interpolated using the following
polynomial.
![]() denoting the [001] direction, one obtains for the polar angle
denoting the [001] direction, one obtains for the polar angle
![]() that relates two given vectors
that relates two given vectors
![]() and
and
![]() by
by
![]() has no unique solution. In
two dimensions, this vector equation denotes two scalar equations, whereas the
2 by 2 matrix
has no unique solution. In
two dimensions, this vector equation denotes two scalar equations, whereas the
2 by 2 matrix
![]() has four unknown elements. The straightforward
assumption of a diagonal matrix with diagonal elements
has four unknown elements. The straightforward
assumption of a diagonal matrix with diagonal elements
![]() and
and
![]() cannot be made, because this definition
becomes singular whenever the driving force vector is parallel to the
cannot be made, because this definition
becomes singular whenever the driving force vector is parallel to the ![]() or
or
![]() axis.
axis.
![]() can be easily found as
can be easily found as
![]() . The four matrix elements can now be uniquely determined from the
following two vector equations.
. The four matrix elements can now be uniquely determined from the
following two vector equations.