The most frequently used distribution is the cosine distribution, which is required to describe the arrival angles of neutral particles (2.5) or diffusive reemission (2.18). The cosine distribution can be seen as a special case of the power cosine distribution (2.6) with ![]() or as a special case of the coned cosine distribution with
or as a special case of the coned cosine distribution with
![]() . As shown in the next section, sampling a cosine distribution using Algorithm 5.2 is faster than using Algorithm 5.3 for the coned cosine distribution. Therefore, the power cosine distribution with
. As shown in the next section, sampling a cosine distribution using Algorithm 5.2 is faster than using Algorithm 5.3 for the coned cosine distribution. Therefore, the power cosine distribution with ![]() is the common technique for sampling a cosine distribution [37]. However, the polar angle is usually not of interest. It is just an intermediate result passed to Algorithm 5.4 to generate a unit vector as needed for ray tracing.
is the common technique for sampling a cosine distribution [37]. However, the polar angle is usually not of interest. It is just an intermediate result passed to Algorithm 5.4 to generate a unit vector as needed for ray tracing.
In the following discussion an alternative method is proposed, which samples a unit vector obeying the cosine distribution directly, without the need of an additional rotation as described in Section 5.3.3. The method uses the fact that the sum of the given direction vector ![]() and a unit random vector
and a unit random vector
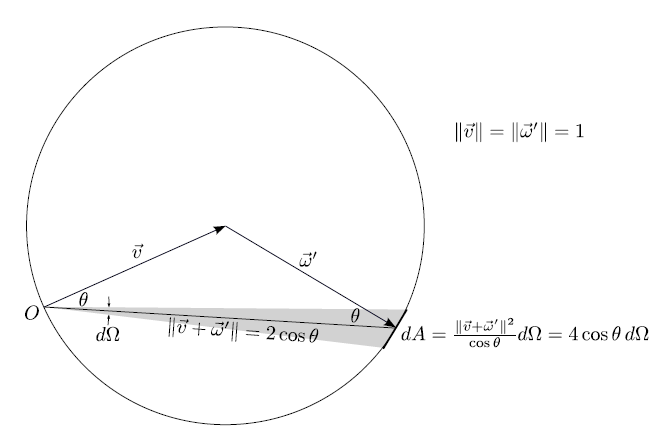
![]() , which is uniformly distributed over a sphere, follows a cosine distribution. As illustrated in Figure 5.6, the area
, which is uniformly distributed over a sphere, follows a cosine distribution. As illustrated in Figure 5.6, the area ![]() seen from the origin
seen from the origin ![]() in a direction with polar angle
in a direction with polar angle ![]() within an infinitesimal solid angle
within an infinitesimal solid angle
![]() is
is
| (5.52) |
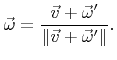 |
(5.53) |
|