The simulation domain for ray tracing is limited in the vertical direction by the source plane
![]() and the surface
and the surface
![]() (see Figure 2.1). The lateral directions are limited by boundary conditions. Periodic and reflective boundary conditions are most commonly used. Both types can easily be incorporated using ray tracing. If a particle would leave the feature-scale region at a periodic boundary, it reenters the simulation domain at the opposite boundary with same direction. In case of reflective boundaries the particle direction is reflected and the trajectory calculation is continued.
(see Figure 2.1). The lateral directions are limited by boundary conditions. Periodic and reflective boundary conditions are most commonly used. Both types can easily be incorporated using ray tracing. If a particle would leave the feature-scale region at a periodic boundary, it reenters the simulation domain at the opposite boundary with same direction. In case of reflective boundaries the particle direction is reflected and the trajectory calculation is continued.
Periodic boundaries can only be applied, if the initial geometry is periodic, which means that opposite sides of the geometry fit together. By contrast, reflective boundaries can be applied regardless of the initial geometry. However, the application of reflective boundaries can be problematic for inclined particle incidence. Due to the reflection at boundaries, particles obtain a different direction than given initially by the arriving flux distribution
![]() , which leads to an incorrect arriving flux distribution
, which leads to an incorrect arriving flux distribution ![]() on the surface. Only if the flux distribution
on the surface. Only if the flux distribution
![]() is symmetric with respect to the vertical grid direction, reflective boundaries can be applied. Hence, for all directions
is symmetric with respect to the vertical grid direction, reflective boundaries can be applied. Hence, for all directions
![]() and
and
![]() satisfying
satisfying
![]() , the corresponding values of the arriving flux distribution need to be equal,
, the corresponding values of the arriving flux distribution need to be equal,
![]() .
.
Problems, for which
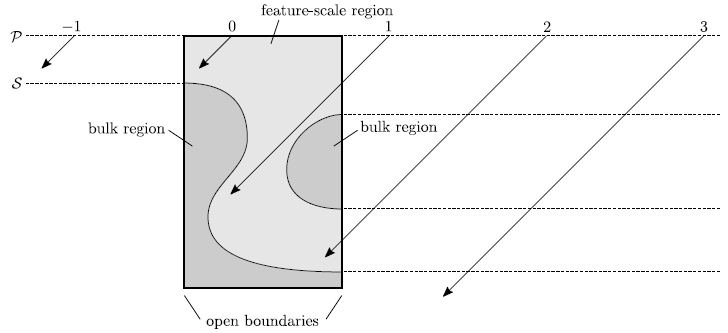
![]() is not symmetric and the initial geometry is not periodic at the same time, neither reflective nor periodic boundaries can be applied. For such problems it is better to use open boundaries, where the geometry is thought to extend to infinity (see Figure 5.2). A particle leaving the simulation domain is not further treated. It is clear that this leads to wrong rates, especially for grid points close to the boundary. Since no particles enter the simulation domain through the boundary, the flux distribution is zero for the corresponding directions. To obtain correct results new particles must be launched from the boundaries. The calculation of the corresponding arriving flux distribution for points on the lateral boundaries is very difficult, because it can be composed of direct flux from the source plane and secondary flux due to reemission.
is not symmetric and the initial geometry is not periodic at the same time, neither reflective nor periodic boundaries can be applied. For such problems it is better to use open boundaries, where the geometry is thought to extend to infinity (see Figure 5.2). A particle leaving the simulation domain is not further treated. It is clear that this leads to wrong rates, especially for grid points close to the boundary. Since no particles enter the simulation domain through the boundary, the flux distribution is zero for the corresponding directions. To obtain correct results new particles must be launched from the boundaries. The calculation of the corresponding arriving flux distribution for points on the lateral boundaries is very difficult, because it can be composed of direct flux from the source plane and secondary flux due to reemission.
|
At least the direct flux can be fully incorporated, if the arriving flux distribution is equally distributed over the source plane
![]() . As usual, particles are randomly initiated from the source plane. However, additional particles of the same species are launched with same direction and energy from positions which are relatively offset by an integral multiple of the domain extension. The number of particle trajectories which must be computed can be limited from the outset, since only particles which intersect the simulation domain have to be considered. In the example shown in Figure 5.2 only the particles with numbers 0, 1, and 2 must be considered.
. As usual, particles are randomly initiated from the source plane. However, additional particles of the same species are launched with same direction and energy from positions which are relatively offset by an integral multiple of the domain extension. The number of particle trajectories which must be computed can be limited from the outset, since only particles which intersect the simulation domain have to be considered. In the example shown in Figure 5.2 only the particles with numbers 0, 1, and 2 must be considered.
The entrance point into the simulation domain can easily be calculated for all particles which are started from the outside. However, it is necessary to check whether the simulation domain can be reached without intersecting the surface before entry. For example, particle 2 is not able to reach the surface within the simulation domain, because it would have to traverse the bulk region (which is extended to infinity). Therefore, each particle, starting from the outside, is initially traced along the boundary of the simulation domain, until it reaches the entrance point, in order to check, if it encounters any surface intersection.
If the arriving flux distribution
![]() is not equally distributed over the source plane
is not equally distributed over the source plane
![]() , but rather locally concentrated, as is the case for focused ion beam (FIB) applications, the choice of boundary condition does not affect the result, assuming the lateral extensions of the simulation domain are sufficiently large.
, but rather locally concentrated, as is the case for focused ion beam (FIB) applications, the choice of boundary condition does not affect the result, assuming the lateral extensions of the simulation domain are sufficiently large.