If the quantum-mechanical nature of electrons is neglected, carrier transport
in a device can be described by BOLTZMANN's transport equation which is a seven-dimensional
integro-differential equation in the phase space [46]. For
electrons it reads
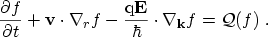 |
(2.2) |
Here,
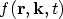 is the distribution of carriers in space
(
is the distribution of carriers in space
(
 ), momentum (
), momentum (
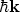 ), and time. On the right-hand side
of this partial differential equation stands the collision operator
), and time. On the right-hand side
of this partial differential equation stands the collision operator
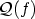 which describes scattering of particles due to phonons,
impurities, interfaces, or other scattering sources.
However, the direct solution of this equation is computationally
prohibitive2.7. It is
rather solved by approximate means applying the method of moments or using
methods. In the method of moments each term of (2.2) is
multiplied with a weight function and integrated over
which describes scattering of particles due to phonons,
impurities, interfaces, or other scattering sources.
However, the direct solution of this equation is computationally
prohibitive2.7. It is
rather solved by approximate means applying the method of moments or using
methods. In the method of moments each term of (2.2) is
multiplied with a weight function and integrated over
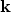 -space. This
yields a set of differential equations in the (
-space. This
yields a set of differential equations in the (
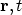 )-space. The
moments of the distribution function are defined by [54]
)-space. The
moments of the distribution function are defined by [54]
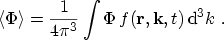 |
(2.3) |
Subsections
A. Gehring: Simulation of Tunneling in Semiconductor Devices