



Next: 6.1.2 Operation Principle
Up: 6.1 Fundamentals
Previous: 6.1 Fundamentals
The state of the EM field is uniquely determined by the Maxwell equations,
which hold at every point in whose neighborhood the physical properties
of the medium are continuous [11, pp. 1-7]:
These four equations have to be supplemented by material equations also
called constitutive relations which describe the behavior of the medium under
the influence of the EM field. In our case the materials, i.e., the resist and
the nonplanar wafer portions, are isotropic, inhomogeneous, linear and
time-invariant.a
The constitutive relations thus take the relatively simple form
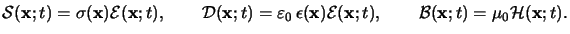 |
(6.1) |
Insertion of these relations into the first and second Maxwell equations gives
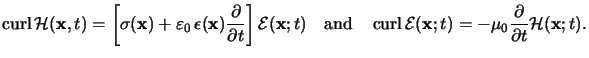 |
(6.2) |
As the incident EM disturbance is a time-harmonic one we employ the
complex phasor notation already used in previous chapters
(cf. (4.1) or (5.22)), i.e.,
![$\displaystyle \mathcal{E}(\mathbf{x};t)= \operatorname{Re}\!\left[\mathbf{E}(\m...
...bf{x};t)= \operatorname{Re}\!\left[\mathbf{H}(\mathbf{x})e^{-j\omega t}\right].$](img818.gif) |
(6.3) |
Hence the first two Maxwell equations (6.3) write
in phasor notation as
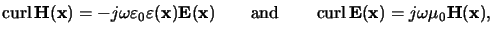 |
(6.4) |
whereby the complex-valued relative permittivity
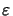 (x) is
defined by
(x) is
defined by
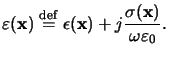 |
(6.5) |
The permittivity
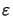 (x) is simply related to the refractive index
n(x) by Maxwell's formula given in (5.23).
(x) is simply related to the refractive index
n(x) by Maxwell's formula given in (5.23).
The electric and magnetic phasor,
E(x) and
H(x), respectively, are related by the two coupled,
first-order PDEs of (6.5). These PDEs are the time-harmonic
versions of the first and second Maxwell equations. The third and fourth Maxwell
equations are automatically satisfied by any solution of (6.5)
or, respectively, of (6.3).
However, an interesting phenomenon follows from
the third Maxwell equation. Due to the conductivity of the materials considered
a charge density is generated by any EM disturbance incident from
outside. In case of a homogeneous conducting material the induced
charge density can be neglected as it falls
off exponentially with time, whereby the relaxation time is very much shorter
than the periodic time of the field vibration [11, pp. 612-615].
In an inhomogeneous conductive material a time-harmonic fluctuation is
superposed to this almost instantaneously vanishing transient term.
This situation can be accounted for by replacing the real-valued permittivity
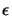 (x) in the third Maxwell equation by its
complex-valued pendant
(x) in the third Maxwell equation by its
complex-valued pendant
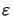 (x) (cf. (6.6)). Then
the third and fourth Maxwell equations take the form
(x) (cf. (6.6)). Then
the third and fourth Maxwell equations take the form
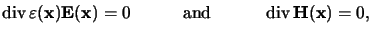 |
(6.6) |
and are thus automatically satisfied by any solution of (6.5).
They do not carry any additional physical information or importance
and thus do not have to be considered separately.
Footnotes
- ...
time-invariant.a
- The resist is essentially an optically nonlinear
material since it changes its properties during exposure. However, the
assumptions made throughout the quasi-static approach transform the nonlinear
problem to a number of inhomogeneous but linear ones
(cf. Section 5.1.4).




Next: 6.1.2 Operation Principle
Up: 6.1 Fundamentals
Previous: 6.1 Fundamentals
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
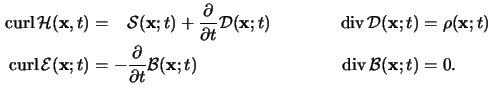
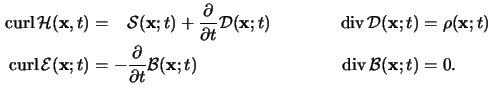
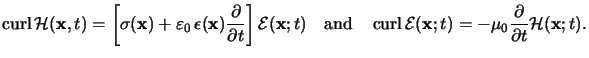
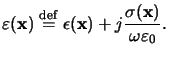
![]() (x) in the third Maxwell equation by its
complex-valued pendant
(x) in the third Maxwell equation by its
complex-valued pendant
![]() (x) (cf. (6.6)). Then
the third and fourth Maxwell equations take the form
(x) (cf. (6.6)). Then
the third and fourth Maxwell equations take the form