6.1.2 Operation Principle

In the previous section it is shown that the time-harmonic Maxwell equations in the form of (6.5) have to be solved. The main difficulties arise from the inhomogeneous permittivity 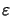$\varepsilon$(x) in (6.6). Otherwise the Maxwell equations could easily be reduced to the Helmholtz equation (4.2) which has a mathematically much simpler structure and can thus be solved very efficiently. However, we have to directly tackle the Maxwell equations. In this section we will outline the main ideas behind the differential method. As the choice of the simulation domain and the BCs resulting thereof are of crucial importance for the operation principle we will discuss them first.

The differential method requires a rectangular-shaped simulation domain, i.e.,

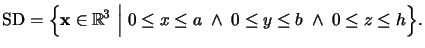$$\mathrm{SD}=\Big\{ \mathbf{x}\in\mathbb{R} ^3 \;\Big\vert\; 0\le x\le a \;\wedge\; 0\le y\le b \;\wedge\; 0\le z\le h \Big\}.$$ (6.7)

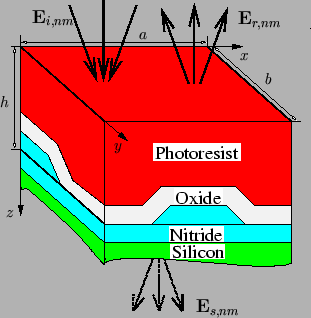
Inside the simulation domain arbitrary inhomogeneous and nonplanar regions can be simulated, above vacuum is situated, and below multiple planar homogeneous layers form a stratified medium. A schematic of a typical formation is shown in Figure 6.1. We now assume that the rectangular domain is one period (a x b x h) of a laterally periodic geometry. Hence the BCs in lateral directions require equal field values at the left and right boundaries as well as in the front and at the back of the structure (cf. Figure 6.1), i.e.,

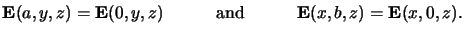$$\mathbf{E}(a,y,z) = \mathbf{E}(0,y,z) \quad\qquad\text{and}\qquad\quad\mathbf{E}(x,b,z) = \mathbf{E}(x,0,z).$$ (6.8)

On top planar waves E_{i, nm} are incident that are modulated by the mask and thus carry the information to be printed. Due to the abrupt change of the optical properties at the air/resist interface reflected waves E_{r, nm} occur. Part of the incident light penetrates into the wafer and propagates through it. At the bottom either lie multiple planar homogeneous layers or only the substrate that is assumed to be infinitely extended since it is typically highly absorptive like silicon. In the former case waves are incident also at the bottom side of the simulation domain since they are reflected within the stratified medium. This situation can be treated analytically using the methods presented in Appendix C. However, in the bottom-most layer, i.e., the substrate, only outgoing waves E_{s, nm} are emitted. In the latter case this situation occurs directly below the simulation domain, which slightly simplifies the formulation of the BCs. Both situations will be discussed below.

  

Figure 6.1: Simulation domain of the differential method. The simulation domain is assumed to be one period (a x b x h) of a laterally periodic structure. In the example given it consists of the inhomogeneous resist, the nonplanar oxide, and the nonplanar part of the nitride. The planar part of the nitride forms with the infinitely extended silicon substrate a stratified medium. Above the resist we have to consider incident E_{i, nm} and reflected E_{r, nm} waves, whereas below the nitride layer only outgoing waves E_{s, nm} travel into the silicon substrate.

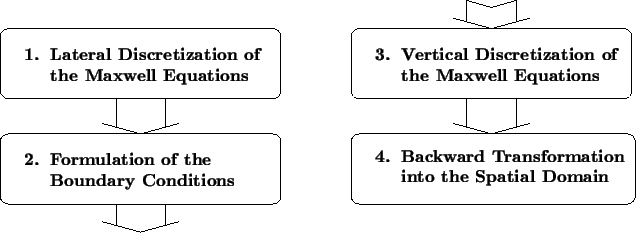
The discretization employed in the differential method basically involves four consecutive steps. In the following enumeration each of them is briefly described:

1.

Lateral Discretization of the Maxwell equations. The dependence of the EM field on the lateral x- and y-coordinates is expressed by Fourier series, i.e., a laterally periodic field distribution is assumed, 

 

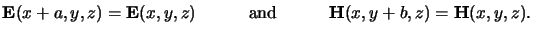$$\mathbf{E}(x+a,y,z) = \mathbf{E}(x,y,z) \quad\qquad\text{and}\qquad\quad \mathbf{H}(x,y+b,z) = \mathbf{H}(x,y,z).$$ (6.9)

A prerequisite for that are a periodic excitation at the top of the structure as well as periodic material properties. Since both the mask and the wafer are assumed to be periodic either requirement is fulfilled and the Fourier expansion of the field is justified. Insertions of these expansions into the time-harmonic Maxwell equations transform the PDEs into ordinary ones. The unknowns of these equations are the Fourier coefficients of the lateral electric and magnetic field vector components.

2.

  Formulation of the Boundary Conditions. The BCs for the system of ODEs thus obtained are found by matching the Fourier expansions valid inside the simulation domain with the Rayleigh expansions valid outside. Algebraic equations are set up that relate each pair of Fourier coefficients belonging together. Exactly half of the BCs are found at the top and at the bottom of the simulation domain. Hence we have to solve a two-point BVP.

3.

  Vertical Discretization of the Maxwell equations. The vertical discretization of this two-point BVP is accomplished by the memory-saving shooting method. This algorithm can be implemented in a particularly efficient way in the situation of partially coherent illumination since the extra numerical costs cause multiple right-hand sides in the final discretized system and are therefore negligible in comparison to the overall costs. Additionally, sophisticated numerical techniques enforce good convergence in even strongly absorptive media.

4.

Backward Transformation into Spatial Domain. The solution vector of the ODE system comprises the vertically dependent Fourier coefficients. These coefficients have to be transformed back into the spatial domain. In case of partially coherent illumination the various contributions representing one source point have to be superposed incoherently to build up the absorbed light intensity within the photoresist needed for the exposure/bleaching model (cf. Abbe's method discussed in Section 4.3.1).

Detailed information on the first three steps is given in the following three sections. The last step is obvious and is therefore not discussed in an own section. In Figure 6.2 the discretization procedure is illustrated graphically.

  

Figure 6.2: Discretization procedure of the differential method. Basically four consecutive steps are involved. The lateral discretization is performed by transforming the partial differential equations into the frequency domain. Once the boundary conditions are established, the obtained ordinary differential equation system is numerically solved. Finally, the calculated Fourier coefficients are transformed back to the spatial domain.