



Next: 6.3.3 Vector-Matrix Notation
Up: 6.3 Formulation of the
Previous: 6.3.1 Air/Resist Interface
A similar derivation applies to the lower interface between resist and
substrate at z = h. There are two different situations as either
only one layer representing the substrate or multiple planar homogeneous layers
forming a stratified medium have to be considered.
The first situation is self-evident and yields BCs totally equivalent
to (6.40), i.e., we obtain
There are two differences between (6.40) and (6.41):
Firstly, no light is incident at the lower interface since the substrate is
assumed to be infinitely extended, i.e., we have homogeneous BCs.
Secondly, the vertical wavevector component
kz, s, nm depends on the
permittivity
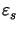 of the substrate material, i.e.,
kz, s, nm =
of the substrate material, i.e.,
kz, s, nm = ![$ \sqrt{\smash[b]{k_0^2\varepsilon_s - k_{x,n}^2 - k_{y,m}^2}}$](img897.gif) . Furthermore,
it has the opposite sign since the lower interface is ``mirrored'' in comparison
to the upper one. Finally, the Rayleigh expansion of the electric field phasor
inside the substrate takes the form
. Furthermore,
it has the opposite sign since the lower interface is ``mirrored'' in comparison
to the upper one. Finally, the Rayleigh expansion of the electric field phasor
inside the substrate takes the form
![$\displaystyle \mathbf{E}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\mathb...
...} e^{+jk_{z,s,nm}(z-h)}\Big] e^{j(k_{x,n}x+k_{y,m}y)}\qquad\text{for}\quad z>h,$](img898.gif) |
(6.29) |
whereby
Es, nm refers to the wave amplitudes traveling into
the substrate (cf. Fig. 6.1).
In the second situation, i.e., when multiple homogeneous layers form a
stratified medium lying below the simulation domain--an example is illustrated
in Fig. 6.1,--the BCs are
derived as follows: Due to the reflections occurring inside the layer stack light
is reflected back to the resist/substrate interface. Therefore also ``incident''
waves have to be taken into account at z = h. The Rayleigh expansion inside the
top-most layer (TL) close to the interface takes the form
![$\displaystyle \mathbf{E}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\mathb...
...},nm}(z-h)}\Big] e^{j(k_{x,n}x+k_{y,m}y)}\text{for}\quad h<z<h+h_{\mathrm{TL}}.$](img899.gif) |
(6.30) |
In Appendix C is shown how to treat multiple homogeneous layers
analytically. Especially (C.26) describes the lateral electric
field amplitudes occurring inside the top-most layer--in (C.26)
the top-most layer refers to air--and relates them to the amplitudes inside
the bottom-most layer representing the substrate via the so-called
propagation matrix
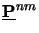 . Hence, the same arguments
that led to (C.27) and (C.28) apply, and the lateral
components of the amplitudes
E+TL, nm and
E-TL, nm propagating downwards and upwards the top-most
layer are related by (cf. (C.28))
The propagation matrix
. Hence, the same arguments
that led to (C.27) and (C.28) apply, and the lateral
components of the amplitudes
E+TL, nm and
E-TL, nm propagating downwards and upwards the top-most
layer are related by (cf. (C.28))
The propagation matrix
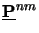 of the stratified medium
depends on the index pair (n, m) since it is determined by the harmonic
frequencies
kx, n = 2
of the stratified medium
depends on the index pair (n, m) since it is determined by the harmonic
frequencies
kx, n = 2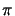 n/a and
ky, m = 2
n/a and
ky, m = 2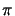 m/b. This
means that each harmonic has its own propagation matrix
m/b. This
means that each harmonic has its own propagation matrix
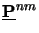 .
.
In addition to (6.44) four relations
corresponding to ``mirrored'' versions of (6.38) and
(6.39) must also be stratified at z = h:
and
In total, (6.44) to (6.46) constitute six
equations for each harmonic frequency (n, m). In these six relations the
four lateral amplitude components of the waves
E+TL, nm
and
E-TL, nm propagating inside the top-most layer are
unknown. Hence they have to be eliminated analytically and we finally obtain
whereby the two factors mx and my describe the influence of the
stratified medium and are given by
The two relations of (6.47) constitute
NODE/2
BCs in case of multiple planar homogeneous layers below
the simulation domain. Comparing them with the BCs
(6.41) valid for the substrate-only-situation shows that
the difference lies in the two factors mx and my. They can easily
be calculated in advance, and thus multiple planar layers below
the resist can be treated in a very efficient way.
Finally, it should be noted that the general formulation (6.47)
holds in both cases since in the substrate-only-situation we have
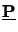 =
= 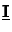 and the two coefficients mx and my are unity,
i.e., mx = my = 1 and (6.41) and (6.47) are identical.
and the two coefficients mx and my are unity,
i.e., mx = my = 1 and (6.41) and (6.47) are identical.




Next: 6.3.3 Vector-Matrix Notation
Up: 6.3 Formulation of the
Previous: 6.3.1 Air/Resist Interface
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
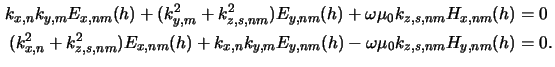
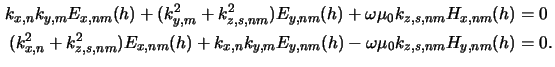
![$\displaystyle \mathbf{E}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\mathb...
...} e^{+jk_{z,s,nm}(z-h)}\Big] e^{j(k_{x,n}x+k_{y,m}y)}\qquad\text{for}\quad z>h,$](img898.gif)
![$\displaystyle \mathbf{E}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\mathb...
...},nm}(z-h)}\Big] e^{j(k_{x,n}x+k_{y,m}y)}\text{for}\quad h<z<h+h_{\mathrm{TL}}.$](img899.gif)
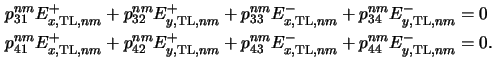
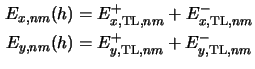
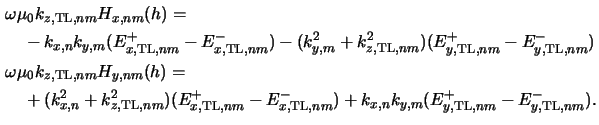
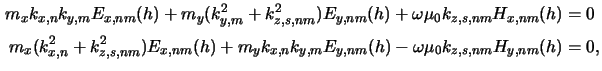
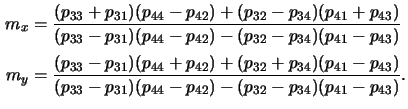
![]() =
= ![]() and the two coefficients mx and my are unity,
i.e., mx = my = 1 and (6.41) and (6.47) are identical.
and the two coefficients mx and my are unity,
i.e., mx = my = 1 and (6.41) and (6.47) are identical.