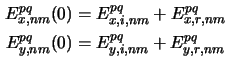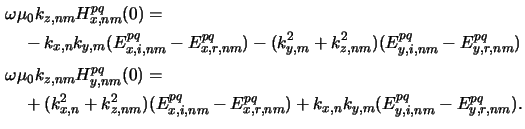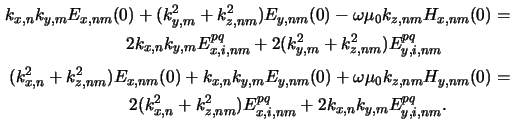Next: 6.3.2 Resist/Substrate Interface
Up: 6.3 Formulation of the
Previous: 6.3 Formulation of the
Above the air/resist interface, i.e., for z > 0, the light consists of
incoming
Ei, nmpq and reflected waves
Er, nmpq
(c.f. Figure 6.1). As outlined in Section 4.1.5
in combination with the vector-valued aerial image simulation
the incident electric field vector
Eipq(x) is given by the Rayleigh expansion of
(4.55), whereby the superscript (p, q) refers to the source
point considered. Due to the assumption of a periodic simulation domain
also the reflected light
Erpq(x) can be represented by a
Rayleigh expansion. Hence the field distribution above the simulation domain,
which is due to one source point, follows from the superposition of two
Rayleigh expansions and writes to
![$\displaystyle \mathbf{E}^{pq}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\...
...}^{pq} e^{-jk_{z,nm}z} \Big] e^{j(k_{x,n}x+k_{y,m}y)}\qquad\text{for}\quad z<0.$](img888.gif) |
(6.28) |
Note that we have already used truncated expansions, which is no
approximation as long as the set
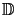 2 comprises all incident waves.
In any reasonable simulation application this will be the case.
2 comprises all incident waves.
In any reasonable simulation application this will be the case.
Since the transversal electric field components must be continuous across the
interface [11, p. 6] we obtain
for the Fourier coefficients of the
lateral electric field components right at the upper boundary at z = 0.
With the transverseness property of homogeneous plane waves, i.e.,
Enm 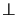 Hnm
Hnm 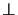 knm, the magnetic
wave amplitudes can easily be calculated from the electric ones.
The lateral magnetic field components must be continuous, too.
Performing the same derivation as in Appendix C that
resulted in (C.7), we obtain for the lateral components of the
Fourier coefficients of the magnetic field
Hpq(x):
knm, the magnetic
wave amplitudes can easily be calculated from the electric ones.
The lateral magnetic field components must be continuous, too.
Performing the same derivation as in Appendix C that
resulted in (C.7), we obtain for the lateral components of the
Fourier coefficients of the magnetic field
Hpq(x):
The two equations (6.38) and (6.39) establish four
relations for each index pair (n, m) of the
(2Nx + 1) x (2Ny + 1) Fourier
coefficients. This means that we have already derived
NODE = 4 x (2Nx + 1) x (2Ny + 1) BCs
(cf. (6.29)).
However, the lateral coefficients
Erx, nm and
Ery, nm of
the reflected light
are unknown in (6.38) and (6.39).
Hence we have to eliminate them and end up at
NODE/2 conditions
for the upper interface z = 0 that write to
To clarify the number of equations that are represented by (6.40):
There are
(2Nx + 1) x (2Ny + 1) index-pairs (n, m) and two equations, one
for each lateral direction x and y. Thus (6.40) represents
2 x (2Nx + 1) x (2Ny + 1) or
NODE/2
BCs valid at z = 0.




Next: 6.3.2 Resist/Substrate Interface
Up: 6.3 Formulation of the
Previous: 6.3 Formulation of the
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
![$\displaystyle \mathbf{E}^{pq}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\...
...}^{pq} e^{-jk_{z,nm}z} \Big] e^{j(k_{x,n}x+k_{y,m}y)}\qquad\text{for}\quad z<0.$](img888.gif)
![$\displaystyle \mathbf{E}^{pq}(\mathbf{x}) = \sum_{(n,m)\in\mathbb{D} ^2} \Big[\...
...}^{pq} e^{-jk_{z,nm}z} \Big] e^{j(k_{x,n}x+k_{y,m}y)}\qquad\text{for}\quad z<0.$](img888.gif)