



Next: 6.1.2 Analytische Lösung
Up: 6.1 Elektronenbeweglichkeit
Previous: 6.1 Elektronenbeweglichkeit
Der theoretischen Bestimmung von  liegt die Boltzmanngleichung zugrunde, aus der auch die oben genannten Transportmodelle rigoros abgeleitet werden können. Ursprünglich aus der kinetischen Gastheorie stammend, ist ihre Gültigkeit zum Zweck der Beschreibung des Stromtransports in HL generell anerkannt [76].
Sie ist eine Bestimmungsgleichung für die mikroskopische Verteilungsfunktion
liegt die Boltzmanngleichung zugrunde, aus der auch die oben genannten Transportmodelle rigoros abgeleitet werden können. Ursprünglich aus der kinetischen Gastheorie stammend, ist ihre Gültigkeit zum Zweck der Beschreibung des Stromtransports in HL generell anerkannt [76].
Sie ist eine Bestimmungsgleichung für die mikroskopische Verteilungsfunktion 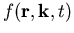 . f ist proportional der Verteilung (Dichte) der Elektronen im Ortsraum (``real space'') und Impulsraum (``k-space'') zum Zeitpunkt t.
Die Summation über die Zustände im
. f ist proportional der Verteilung (Dichte) der Elektronen im Ortsraum (``real space'') und Impulsraum (``k-space'') zum Zeitpunkt t.
Die Summation über die Zustände im 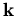 -Raum, die als Integration über
-Raum, die als Integration über 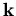 geschrieben wird, ergibt daher die Elektronenkonzentration n,
geschrieben wird, ergibt daher die Elektronenkonzentration n,
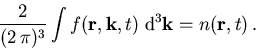 |
(6.2) |
Die Integration über 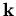 kann auch allgemein in ein Integral in der Energievariablen übergeführt werden, wie dies in Abschnitt 3.2.1 für die Ladungsträgerkonzentration beschrieben wurde. Es gilt
kann auch allgemein in ein Integral in der Energievariablen übergeführt werden, wie dies in Abschnitt 3.2.1 für die Ladungsträgerkonzentration beschrieben wurde. Es gilt
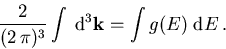 |
(6.3) |
Ist f bekannt, können durch Mittelwertbildung daraus sämtliche Observablen bestimmt werden. Mittelwerte über die Verteilungsfunktion wie in (6.2) schreibt man üblicherweise kurz mit spitzen Klammern, sodaß gilt
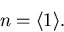 |
(6.4) |
Die Elektronenkonzentration ist das nullte Moment ![[*]](foot_motif.gif) von f.
von f.
Die Boltzmanngleichung beschreibt die totale zeitliche Änderung von f
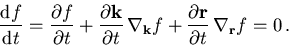 |
(6.5) |
In semiklassischer Näherung wird ein Elektron dabei als konzentriertes Teilchen betrachtet, das zwischen statistischen Streuvorgängen den äußeren Kräften klassisch unterworfen ist.
Der zweite Term in (6.5) ist daher zerlegbar in einen Anteil zufolge der äußeren Kräfte 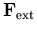 und einen Anteil zufolge der inhärenten Streuung im Kristall, die man durch
und einen Anteil zufolge der inhärenten Streuung im Kristall, die man durch 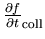 bezeichnet,
bezeichnet,
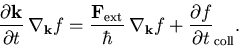 |
(6.6) |
Der Kollisionsterm ist allgemein gegeben durch das Streuintegral
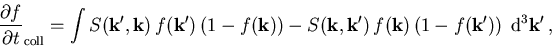 |
(6.7) |
wobei 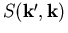 die Wahrscheinlichkeit des Übergangs vom Zustand
die Wahrscheinlichkeit des Übergangs vom Zustand 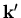 nach
nach 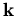 angibt. Der erste Integralterm in (6.7) bezeichnet also Vorgänge, die in den Zustand
angibt. Der erste Integralterm in (6.7) bezeichnet also Vorgänge, die in den Zustand 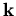 hineinstreuen. Die Faktoren (1-f) bedeuten die Wahrscheinlichkeit, daß der Endzustand unbesetzt ist, und berücksichtigen somit das Pauli Prinzip .
Die Streuwahrscheinlichkeiten
hineinstreuen. Die Faktoren (1-f) bedeuten die Wahrscheinlichkeit, daß der Endzustand unbesetzt ist, und berücksichtigen somit das Pauli Prinzip .
Die Streuwahrscheinlichkeiten 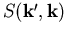 für die einzelnen Streuprozesse sind aus der Quantenmechanik herleitbar.
für die einzelnen Streuprozesse sind aus der Quantenmechanik herleitbar.
Obige Formulierung impliziert, daß die Streuvorgänge strikt lokal und instantan den Impuls der Ladungsträger ändern.
Die Bandstruktur, die die Bewegung des Elektrons bestimmt, geht auch explizit in den dritten Term von (6.5) ein,
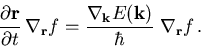 |
(6.8) |
Wie auch aus prinzipiellen Überlegungen der statistischen Mechanik folgt, ist die Distribution im thermodynamischen Gleichgewicht f0 (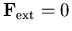 ) die Fermi-Dirac Verteilung.
Für nicht entartete HL ist die Annahme gültig, daß die Endzustände immer frei sind. Dies bedeutet
) die Fermi-Dirac Verteilung.
Für nicht entartete HL ist die Annahme gültig, daß die Endzustände immer frei sind. Dies bedeutet 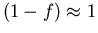 , und f0 geht in die Maxwell-Boltzmann Verteilung über.
In diesem Fall läßt sich der Anteil, der aus dem Zustand
, und f0 geht in die Maxwell-Boltzmann Verteilung über.
In diesem Fall läßt sich der Anteil, der aus dem Zustand 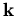 herausstreut, separieren in das Produkt
herausstreut, separieren in das Produkt 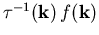 , wobei
, wobei
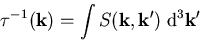 |
(6.9) |
die totale Streurate im Zustand 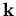 ist.
ist.
Im stationären und homogenen Fall (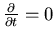 ,
, 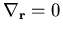 ) reduziert sich (6.5) zu
) reduziert sich (6.5) zu
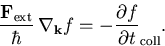 |
(6.10) |
Selbst die Lösung von (6.10) ist durch den Kollisionsterms außerordentlich schwierig, drastische Annahmen sind dabei nötig. Für den Bereich des Ohmschen Transports sind analytische Ausdrücke für einige Spezialfälle herleitbar (siehe Abschnitt 6.1.2). Die numerische Lösung mit Hilfe der Monte Carlo Methode wird in Abschnitt 6.1.3 erläutert.




Next: 6.1.2 Analytische Lösung
Up: 6.1 Elektronenbeweglichkeit
Previous: 6.1 Elektronenbeweglichkeit
Christian Koepf
1997-11-11
![[*]](foot_motif.gif) von f.
von f.![]() ) die Fermi-Dirac Verteilung.
Für nicht entartete HL ist die Annahme gültig, daß die Endzustände immer frei sind. Dies bedeutet
) die Fermi-Dirac Verteilung.
Für nicht entartete HL ist die Annahme gültig, daß die Endzustände immer frei sind. Dies bedeutet ![]() , und f0 geht in die Maxwell-Boltzmann Verteilung über.
In diesem Fall läßt sich der Anteil, der aus dem Zustand
, und f0 geht in die Maxwell-Boltzmann Verteilung über.
In diesem Fall läßt sich der Anteil, der aus dem Zustand ![]() herausstreut, separieren in das Produkt
herausstreut, separieren in das Produkt ![]() , wobei
, wobei
![]() ,
, ![]() ) reduziert sich (6.5) zu
) reduziert sich (6.5) zu