


Next: 3.7 Generation and Recombination
Up: 3.6 Energy Relaxation Time
Previous: 3.6.1 Methodology
Subsections
The following expression is used to model the electron relaxation time as a
function of the carrier and lattice temperatures:
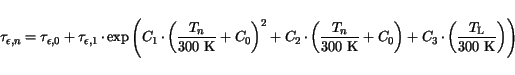 |
(3.138) |
In case of holes a constant energy relaxation time is assumed.
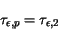 |
(3.139) |
The flexibility of this function allows its easy adaption to all considered
materials. For Si, Ge, and III-V binary materials, all parameters in
(3.138) are summarized in Table 3.33.
Table 3.33:
Parameter values for the energy relaxation time model for basic materials
| Material |
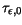 [ps] [ps] |
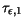 [ps] [ps] |
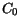 |
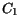 |
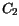 |
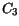 |
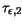 [ps] [ps] |
| Si |
1.0 |
-0.538 |
0 |
0.0015 |
-0.09 |
0.17 |
0.4 |
| Ge |
0.26 |
1.49 |
0 |
-0.434 |
1.322 |
0 |
0.4 |
| GaAs |
0.48 |
0.025 |
0 |
-0.053 |
0.853 |
0.5 |
1.0 |
| AlAs |
0.17 |
0.025 |
61 |
-0.053 |
0.853 |
0.5 |
1.0 |
| InAs |
0.08 |
0.025 |
3 |
-0.053 |
0.853 |
0.5 |
1.0 |
| InP |
0.5 |
0.21 |
-18 |
-0.04 |
0 |
0 |
1.0 |
| GaP |
0.04 |
0.21 |
10 |
-0.04 |
0 |
0 |
1.0 |
|
In the case of III-V semiconductor alloys the dependence of
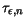 on the
material composition
on the
material composition 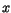 is included.
is included.
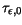 and
and 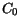 are modeled as a
quadratic function of
are modeled as a
quadratic function of 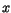 . The parameters are summarized in Table 3.34.
. The parameters are summarized in Table 3.34.
The direct method is used for Si, Ge and GaAs, and the indirect one for AlAs
and InAs, depending on the MC data available. Fig. 3.40 shows the values for
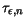 in Si obtained from the model (lines) and Monte-Carlo results (circles
and triangles) at different lattice temperatures. The energy relaxation time
slightly decreases with increasing lattice temperature. It is also observed
that for high electron temperatures,
in Si obtained from the model (lines) and Monte-Carlo results (circles
and triangles) at different lattice temperatures. The energy relaxation time
slightly decreases with increasing lattice temperature. It is also observed
that for high electron temperatures,
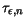 tends to saturate.
tends to saturate.
At very low electron temperature
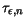 starts to increase. This effect is
not reproduced by the model. When the electron temperature is close to the
lattice temperature, the term
starts to increase. This effect is
not reproduced by the model. When the electron temperature is close to the
lattice temperature, the term
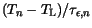 appearing in the energy
balance tends to zero [183], thus the influence of
appearing in the energy
balance tends to zero [183], thus the influence of
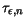 is
negligible, and therefore its increase can be neglected.
is
negligible, and therefore its increase can be neglected.
In GaAs and Ge similar behavior was observed at very low electron temperature,
and the same assumptions as for Si are made. In the case of Ge Fig. 3.41
shows that
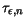 is nearly independent of the lattice temperature, except
for very low electron temperature. Therefore, any lattice temperature
dependence is neglected (
is nearly independent of the lattice temperature, except
for very low electron temperature. Therefore, any lattice temperature
dependence is neglected (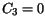 in (3.138)). The sharp initial
fall is attributed to the increase of optical and inter valley scattering as
the electrons are heated by the field [186].
in (3.138)). The sharp initial
fall is attributed to the increase of optical and inter valley scattering as
the electrons are heated by the field [186].
The results for GaAs are shown in Fig. 3.42. At high electron
temperatures
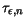 tends to some saturated value and becomes independent of
the lattice temperature. For low and intermediate electron temperatures, the
behavior can be attributed to the transition of electrons from the
tends to some saturated value and becomes independent of
the lattice temperature. For low and intermediate electron temperatures, the
behavior can be attributed to the transition of electrons from the 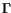 to
the
to
the 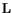 valleys. The electron temperature for which
valleys. The electron temperature for which
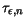 reaches the peak
value is independent of the lattice temperature. The associated average energy,
reaches the peak
value is independent of the lattice temperature. The associated average energy,
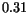 eV, is close to the energy difference between the two valleys,
eV, is close to the energy difference between the two valleys, 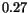 eV.
eV.
Figure 3.40:
Energy relaxation time as a function of electron temperature:
Comparison of the model and MC data for Si at several lattice temperatures
|
|
Figure 3.41:
Energy relaxation time as a function of electron temperature:
Comparison of the model and MC data for Ge
|
|
Figure 3.42:
Energy relaxation time as a function of electron temperature:
Comparison of the model and MC data GaAs at several lattice temperatures
|
|
The similar behavior of the energy relaxation time
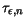 in
In
in
In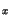 Ga
Ga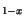 As and Al
As and Al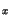 Ga
Ga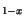 As to that in GaAs can be seen in
Fig. 3.43 and Fig. 3.44. Thus,
As to that in GaAs can be seen in
Fig. 3.43 and Fig. 3.44. Thus,
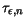 of alloy materials is modeled
by preserving the standard deviation and the amplitude of the function obtained
for GaAs with the direct method and by adjusting then the position with the
material composition dependence of
of alloy materials is modeled
by preserving the standard deviation and the amplitude of the function obtained
for GaAs with the direct method and by adjusting then the position with the
material composition dependence of
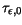 (
(
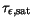 ) and
) and 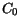 (
(
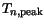 ).
).
For
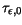 and
and 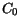 of alloy materials (A
of alloy materials (A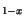 B
B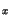 ) the model
suggests a quadratic interpolation between the the values from Table 3.33
for the basic materials (A and B) depending on the material composition
) the model
suggests a quadratic interpolation between the the values from Table 3.33
for the basic materials (A and B) depending on the material composition 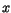 .
.
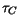 and
and 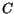 are referred to as bowing parameters. The values used in this
model are summarized in Table 3.34.
are referred to as bowing parameters. The values used in this
model are summarized in Table 3.34.
Table 3.34:
Parameter values for energy relaxation times in alloy materials
| Material |
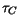 [ps] [ps] |
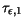 [ps] [ps] |
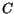 |
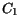 |
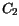 |
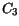 |
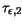 [ps] [ps] |
| AlGaAs |
-0.35 |
0.025 |
-61 |
-0.053 |
0.853 |
0.5 |
1.0 |
| InGaAs |
1.8 |
0.025 |
-34 |
-0.053 |
0.853 |
0.5 |
1.0 |
| InGaP |
-0.4 |
0.21 |
-5.2 |
-0.04 |
0 |
0 |
1.0 |
|
The indirect method is applicable for all semiconductor alloys as explained in
Section 2.2. The lattice temperature dependence of
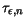 of GaAs is
preserved for both semiconductor alloys considered, Al
of GaAs is
preserved for both semiconductor alloys considered, Al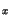 Ga
Ga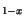 As and
In
As and
In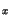 Ga
Ga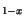 As. This approximation is more accurate for low material
composition, which is more frequently used (
As. This approximation is more accurate for low material
composition, which is more frequently used (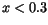 ).
).
In Fig. 3.43 the results of the model for
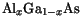 at 300 K for different material compositions
at 300 K for different material compositions 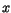 are shown. Note the shift of
the electron temperature, at which
are shown. Note the shift of
the electron temperature, at which
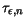 reaches its maximum to lower values
with the increase of
reaches its maximum to lower values
with the increase of 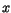 . For high values (
. For high values (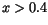 ) no peak value of
) no peak value of
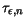 is observed. This behavior can be attributed to the composition dependence of the
is observed. This behavior can be attributed to the composition dependence of the
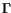 ,
, 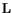 and
and 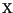 valley minima. When the Al fraction changes from
valley minima. When the Al fraction changes from 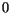 to
to
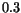 , the energy difference between the
, the energy difference between the 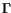 and
and 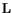 valleys varies
between
valleys varies
between 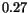 and
and 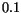 eV. The corresponding change of the electron energy
associated to the peak of
eV. The corresponding change of the electron energy
associated to the peak of
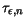 , varies between
, varies between 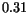 to
to 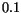 eV. Furthermore, for Al contents
eV. Furthermore, for Al contents 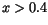 the
the 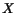 valleys are the lowest ones,
and the bandgap becomes indirect. This explains the absence of a peak of
valleys are the lowest ones,
and the bandgap becomes indirect. This explains the absence of a peak of
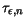 for
for 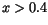 .
.
For In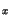 Ga
Ga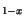 As similar results are obtained in Fig. 3.44. There is
a shift of the maximum
As similar results are obtained in Fig. 3.44. There is
a shift of the maximum
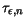 to higher values with increasing
Indium composition up to
to higher values with increasing
Indium composition up to 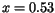 . This can be explained with the electron
population change due to
. This can be explained with the electron
population change due to
 transitions. For InAs a quick shift to
lower values is observed, not explained by the dependence of the energy valleys
on
transitions. For InAs a quick shift to
lower values is observed, not explained by the dependence of the energy valleys
on  . Monte-Carlo simulation results show that at very high Indium contents
the average electron energy decreases and the saturation drift velocity
increases very much, but no clear results are available in this case.
. Monte-Carlo simulation results show that at very high Indium contents
the average electron energy decreases and the saturation drift velocity
increases very much, but no clear results are available in this case.
Figure 3.43:
Energy relaxation time as a function of electron temperature
for different Al contents in AlGaAs at room temperature
|
|
Figure 3.44:
Energy relaxation time as a function of electron temperature
for different In contents in InGaAs at room temperature
|
|
The energy relaxation times are used in the HD mobility model
(3.129) and in the relaxation terms of the energy balance
equations (3.8) and (3.9). Additionally,
if self-heating is included, the energy relaxation times are used in the
relaxation terms of the lattice heat flow equation (3.17).
Using non-constant electron energy relaxation times in
(3.129) allows proper modeling of the velocity overshoot in
the velocity-field characteristics for III-V materials. In addition, it helps
better accuracy for the bias dependence of small-signal parameters to be achieved.
Good agreement with the MC simulation results and its simple
analytical structure make it attractive for device simulation.



Next: 3.7 Generation and Recombination
Up: 3.6 Energy Relaxation Time
Previous: 3.6.1 Methodology
Vassil Palankovski
2001-02-28
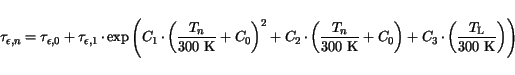
![]() starts to increase. This effect is
not reproduced by the model. When the electron temperature is close to the
lattice temperature, the term
starts to increase. This effect is
not reproduced by the model. When the electron temperature is close to the
lattice temperature, the term
![]() appearing in the energy
balance tends to zero [183], thus the influence of
appearing in the energy
balance tends to zero [183], thus the influence of
![]() is
negligible, and therefore its increase can be neglected.
is
negligible, and therefore its increase can be neglected.
![]() is nearly independent of the lattice temperature, except
for very low electron temperature. Therefore, any lattice temperature
dependence is neglected (
is nearly independent of the lattice temperature, except
for very low electron temperature. Therefore, any lattice temperature
dependence is neglected (![]() in (3.138)). The sharp initial
fall is attributed to the increase of optical and inter valley scattering as
the electrons are heated by the field [186].
in (3.138)). The sharp initial
fall is attributed to the increase of optical and inter valley scattering as
the electrons are heated by the field [186].
![]() tends to some saturated value and becomes independent of
the lattice temperature. For low and intermediate electron temperatures, the
behavior can be attributed to the transition of electrons from the
tends to some saturated value and becomes independent of
the lattice temperature. For low and intermediate electron temperatures, the
behavior can be attributed to the transition of electrons from the ![]() to
the
to
the ![]() valleys. The electron temperature for which
valleys. The electron temperature for which
![]() reaches the peak
value is independent of the lattice temperature. The associated average energy,
reaches the peak
value is independent of the lattice temperature. The associated average energy,
![]() eV, is close to the energy difference between the two valleys,
eV, is close to the energy difference between the two valleys, ![]() eV.
eV.
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CtwSi.eps}}](img641.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CtwGe.eps}}](img642.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CtwGaAs.eps}}](img643.gif)
![]() and
and ![]() of alloy materials (A
of alloy materials (A![]() B
B![]() ) the model
suggests a quadratic interpolation between the the values from Table 3.33
for the basic materials (A and B) depending on the material composition
) the model
suggests a quadratic interpolation between the the values from Table 3.33
for the basic materials (A and B) depending on the material composition ![]() .
.
![]() at 300 K for different material compositions
at 300 K for different material compositions ![]() are shown. Note the shift of
the electron temperature, at which
are shown. Note the shift of
the electron temperature, at which
![]() reaches its maximum to lower values
with the increase of
reaches its maximum to lower values
with the increase of ![]() . For high values (
. For high values (![]() ) no peak value of
) no peak value of
![]() is observed. This behavior can be attributed to the composition dependence of the
is observed. This behavior can be attributed to the composition dependence of the
![]() ,
, ![]() and
and ![]() valley minima. When the Al fraction changes from
valley minima. When the Al fraction changes from ![]() to
to
![]() , the energy difference between the
, the energy difference between the ![]() and
and ![]() valleys varies
between
valleys varies
between ![]() and
and ![]() eV. The corresponding change of the electron energy
associated to the peak of
eV. The corresponding change of the electron energy
associated to the peak of
![]() , varies between
, varies between ![]() to
to ![]() eV. Furthermore, for Al contents
eV. Furthermore, for Al contents ![]() the
the ![]() valleys are the lowest ones,
and the bandgap becomes indirect. This explains the absence of a peak of
valleys are the lowest ones,
and the bandgap becomes indirect. This explains the absence of a peak of
![]() for
for ![]() .
.
![]() Ga
Ga![]() As similar results are obtained in Fig. 3.44. There is
a shift of the maximum
As similar results are obtained in Fig. 3.44. There is
a shift of the maximum
![]() to higher values with increasing
Indium composition up to
to higher values with increasing
Indium composition up to ![]() . This can be explained with the electron
population change due to
. This can be explained with the electron
population change due to
![]() transitions. For InAs a quick shift to
lower values is observed, not explained by the dependence of the energy valleys
on
transitions. For InAs a quick shift to
lower values is observed, not explained by the dependence of the energy valleys
on ![]() . Monte-Carlo simulation results show that at very high Indium contents
the average electron energy decreases and the saturation drift velocity
increases very much, but no clear results are available in this case.
. Monte-Carlo simulation results show that at very high Indium contents
the average electron energy decreases and the saturation drift velocity
increases very much, but no clear results are available in this case.
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CtwAlAs.eps}}](img658.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CtwInAs.eps}}](img659.gif)