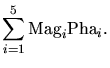5.2.1 Multiple Gaussian Peaks

Prev: 5.2 Benchmarks Up: 5.2 Benchmarks Next: 5.2.2 Reflective Notching

5.2.1 Multiple Gaussian Peaks

The first test example represents a combination of five Gaussian peaks. The superposition of the electric field components can be considered as an ideal phase shifted mask. The main mask opening forms the peak with the highest intensity in the center of the resist volume. The other four peaks represent phase shifted OPC patterns. The intensity of these four peaks is lower and they are shifted towards the corners of the cubic structure. The rate equations sum up as

$\displaystyle \mathrm{Mag_1}$	$\textstyle =$	$\displaystyle 1.0\exp\{-0.01[(x-40)^2+(y-40)^2]\}$
$\displaystyle \mathrm{Mag_2}$	$\textstyle =$	$\displaystyle 0.5\exp\{-0.01[(x-20)^2+(y-20)^2]\}$
$\displaystyle \mathrm{Mag_3}$	$\textstyle =$	$\displaystyle 0.5\exp\{-0.01[(x-20)^2+(y-60)^2]\}$
$\displaystyle \mathrm{Mag_4}$	$\textstyle =$	$\displaystyle 0.5\exp\{-0.01[(x-60)^2+(y-20)^2]\}$
$\displaystyle \mathrm{Mag_5}$	$\textstyle =$	$\displaystyle 0.5\exp\{-0.01[(x-60)^2+(y-60)^2]\}$
$\displaystyle \mathrm{Pha_1}$	$\textstyle =$	$\displaystyle \mathrm{Pha_2}=\mathrm{Pha_3}=\mathrm{Pha_4}=\mathrm{Pha_5}=z$
$\displaystyle r$	$\textstyle =$	$\displaystyle \sum_{i=1}^{5} \mathrm{Mag}_i \mathrm{Pha}_i.$	(5.1)

In these equations, the considered volume has to be subdivided into 80 sections and the position has to be given relatively to this scale. This means, that , , and are given as unitless multiples of 1/80 of the extension of the simulation domain in -, -, and -direction. Therefore the volume where the rates are defined ranges from 0 to 80 in -, -, and -direction and defines the initial resist surface. $\mathrm{Mag}_i$ and $\mathrm{Pha}_i$ represent the impact of magnitudes and phases, respectively, of the electric field components. The final rate summarizes the effects of the different components and is given as normalized etch rate[nm/s]. The same nomenclature and units apply for the two examples following in Section 5.2.2 and Section 5.2.3.

(5.1) gives the overall formula of the interfering intensities for the first test example. The equations describe five Gaussian beams. Fig. 5.2 shows the bird's eye view of the resulting profile after 53s. The uniformly grey plane on top of the simulation domain indicates the initial resist surface with the 5 cones buried downwards into the structure.

**Figure 5.2:** Multiple Gaussian peaks benchmark example.
$\begin{figure}\psfrag{0.8 mu}[b][b][0.8]{0.8 $\mu$m} \psfrag{0.8 um}[t][t][0.8]{... ...s[width=0.5\textwidth]{eps-dev/2-etch3dplot_00053.eps}} \end{center}\end{figure}$

The first observation from Fig. 5.2 is that the cellular algorithm is well suited to develop the circular shape of the Gaussian peaks without facets. Secondly, the Gaussian peaks in close vicinity to each other illustrate an important effect in the evolving surface. The surface normals are continuous for each of the Gaussian peaks, but become undefined at intersections of the beams forming an U-shaped ridge. This is a challenging task for the profile evolution, especially for surface-based simulators. The volume-based cellular implementation implicitly handles such cases.

Prev: 5.2 Benchmarks Up: 5.2 Benchmarks Next: 5.2.2 Reflective Notching

W. Pyka: Feature Scale Modeling for Etching and Deposition Processes in Semiconductor Manufacturing