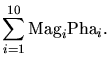5.2.3 Phase Shifted Outriggers

$\displaystyle \mathrm{Mag_1}$	$\textstyle =$	$\displaystyle 1.00\exp\{-0.01[(x-40)^2+(y-40)^2]\}$
$\displaystyle \mathrm{Mag_2}$	$\textstyle =$	$\displaystyle 0.50\exp\{-0.01[(x-20)^2+(y-20)^2]\}$
$\displaystyle \mathrm{Mag_3}$	$\textstyle =$	$\displaystyle 0.50\exp\{-0.01[(x-20)^2+(y-60)^2]\}$
$\displaystyle \mathrm{Mag_4}$	$\textstyle =$	$\displaystyle 0.50\exp\{-0.01[(x-60)^2+(y-20)^2]\}$
$\displaystyle \mathrm{Mag_5}$	$\textstyle =$	$\displaystyle 0.50\exp\{-0.01[(x-60)^2+(y-60)^2]\}$
$\displaystyle \mathrm{Mag_6}$	$\textstyle =$	$\displaystyle 0.10\exp\{-0.01[(x-40)^2+(y-40)^2]\}$
$\displaystyle \mathrm{Mag_7}$	$\textstyle =$	$\displaystyle 0.05\exp\{-0.01[(x-20)^2+(y-20)^2]\}$
$\displaystyle \mathrm{Mag_8}$	$\textstyle =$	$\displaystyle 0.05\exp\{-0.01[(x-20)^2+(y-60)^2]\}$
$\displaystyle \mathrm{Mag_9}$	$\textstyle =$	$\displaystyle 0.05\exp\{-0.01[(x-60)^2+(y-20)^2]\}$
$\displaystyle \mathrm{Mag_{10}}$	$\textstyle =$	$\displaystyle 0.05\exp\{-0.01[(x-60)^2+(y-60)^2]\}$
$\displaystyle \mathrm{Pha_1}$	$\textstyle =$	$\displaystyle \sin(\pi*z/10)$
$\displaystyle \mathrm{Pha_2}$	$\textstyle =$	$\displaystyle \mathrm{Pha_3} = \mathrm{Pha_4} = \mathrm{Pha_5} = \sin(-\pi*z/10+\pi/2)$
$\displaystyle \mathrm{Pha_6}$	$\textstyle =$	$\displaystyle \sin(-\pi*z/10+\pi/2)$
$\displaystyle \mathrm{Pha_7}$	$\textstyle =$	$\displaystyle \mathrm{Pha_8} = \mathrm{Pha_9} = \mathrm{Pha_{10}} = \sin(\pi*z/10)$
$\displaystyle r$	$\textstyle =$	$\displaystyle \sum_{i=1}^{10} \mathrm{Mag}_i \mathrm{Pha}_i.$	(5.3)

Fig. 5.4 shows two different time-steps of the evolving surface. The same perspective as for the example with the defect in Fig. 5.3 is chosen. The front part is again cut away and the outer shape of the evolving front is shaded in black.

This example merges the requirements of the previous two examples including standing waves plus intersecting fronts forming a multitude of tips, ridges and odd structures. Even for this very complex example the cellular approach guarantees the stable evolution of the three-dimensional resist profile. The circular shape of the five beams emerges clearly and the sidewall slope vanishes with increasing development time.

**Figure 5.4:** Phase shifted outriggers benchmark example.
$\begin{figure}\psfrag{0.8 mu}[b][b][0.8]{0.8 $\mu$m} \psfrag{0.8 um}[t][t][0.8]{... ...[width=0.45\textwidth]{eps-dev/5-etch3dplot_00300.eps}} \end{center}\end{figure}$

The regularity of the standing waves in the cellular representation is excellent, which can be observed in the conformity of the openings formed where the evolving front reaches the bounding box at the backside of the simulation domain. Again we encounter regions with undefined surface normals, namely, the ridges on the left hand side of Fig. 5.4, revealing the phase shift between the different beams and the tips formed in the final structure on the right hand side, where four differently oriented planes intersect.