


Next: 4.4 Elementformulierung
Up: 4. Diskretisierung mit Finiten
Previous: 4.2 Das Verfahren von
Unterabschnitte
Man sucht eine Näherungslösung 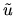 , sodass das Residuum
, sodass das Residuum
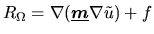 |
(4.18) |
unter Einhaltung der Randbedingungen verschwindet.
Ist die Bedingung 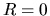 im Gebiet
im Gebiet 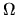 erfüllt, dann hat
man die Lösung mit
erfüllt, dann hat
man die Lösung mit
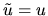 erreicht.
Da der Funktionsraum der Näherungslösungen
erreicht.
Da der Funktionsraum der Näherungslösungen 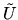 nur eine Teilmenge
des Funktionsraums der exakten Lösungen
nur eine Teilmenge
des Funktionsraums der exakten Lösungen 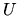 ist, existiert für den
allgemeinen Fall eine solche Lösung nicht.
Deshalb versucht man die Residuumsbedingung nicht exakt zu erfüllen, sondern
gewichtet bzw. gemittelt mit
ist, existiert für den
allgemeinen Fall eine solche Lösung nicht.
Deshalb versucht man die Residuumsbedingung nicht exakt zu erfüllen, sondern
gewichtet bzw. gemittelt mit 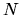 linear unabhängigen
Gewichtsfunktionen (Testfunktionen)
linear unabhängigen
Gewichtsfunktionen (Testfunktionen) 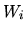 , sodass
, sodass
![$\displaystyle \int_{\Omega}\!\left[W_i\nabla(\makebox{\boldmath$\underline m$}\nabla\tilde u)+W_i f\right]\,\textrm{d}\Omega =0, \qquad i=1, 2, 3, \ldots N\;.$](img224.png) |
(4.19) |
Es liegt nun daran geeignete Gewichtsfunktionen 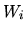 zu wählen, denn von ihnen
hängt die Qualität der Lösung ab.
Z.B. werden bei der Methode der Kollokation Dirac-Impulse
zu wählen, denn von ihnen
hängt die Qualität der Lösung ab.
Z.B. werden bei der Methode der Kollokation Dirac-Impulse
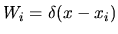 verwendet.
Eine andere gebräuchliche Methode ist es, die Testfunktionen den
Ansatzfunktionen gleichzusetzen
verwendet.
Eine andere gebräuchliche Methode ist es, die Testfunktionen den
Ansatzfunktionen gleichzusetzen 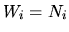 . Diese Methode ist auch als
Galerkin-Ansatz bekannt und soll in dieser Arbeit zur Anwendung
kommen.4.3
. Diese Methode ist auch als
Galerkin-Ansatz bekannt und soll in dieser Arbeit zur Anwendung
kommen.4.3
Da die Konstruktion von Ansatzfunktionen, die sowohl die Dirichlet-
als auch die Neumann-Bedingung exakt erfüllen, sehr schwierig ist,
fordert man, dass lediglich die Dirichlet-Bedingung eingehalten wird.
Damit auch die Neumann-Bedingung näherungsweise erfüllt ist,
berücksichtigt man zusätzlich zum Gebietsresiduum 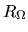 noch ein
Randresiduum
noch ein
Randresiduum 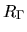
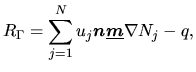 |
(4.20) |
welches mit den Gewichtsfunktionen
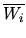 gewichtet wird,
die im Prinzip völlig unabhängig von den
gewichtet wird,
die im Prinzip völlig unabhängig von den 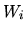 gewählt werden können.
Die unbekannte Koeffizienten der Näherungslösung
gewählt werden können.
Die unbekannte Koeffizienten der Näherungslösung 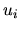 bestimmt man dann aus
der Forderung
bestimmt man dann aus
der Forderung
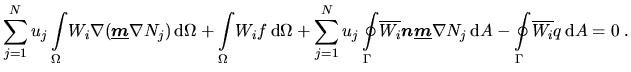 |
(4.21) |
Hierbei ist anzumerken, dass das Randresiduum über den gesamten Rand
des Gebietes (
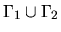 ) gebildet wird--im Gegensatz zum
klassischen Ansatz, wo lediglich über
) gebildet wird--im Gegensatz zum
klassischen Ansatz, wo lediglich über 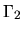 integriert wird.
Die Dirichlet-Bedingung auf
integriert wird.
Die Dirichlet-Bedingung auf 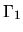 wird hier formal völlig analog
zur Neumann-Bedingung auf
wird hier formal völlig analog
zur Neumann-Bedingung auf 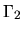 behandelt, allerdings mit einer
vorerst noch unbekannten Konormalableitung
behandelt, allerdings mit einer
vorerst noch unbekannten Konormalableitung 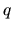 .
Durch diese Vorgehensweise erhält man zwar zunächst ein größeres
Gleichungssystem (Rang
.
Durch diese Vorgehensweise erhält man zwar zunächst ein größeres
Gleichungssystem (Rang 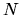 , im Gegensatz zu
, im Gegensatz zu 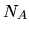 beim klassischen Ansatz),
hat dafür aber später die Möglichkeit eine Näherungslösung für
beim klassischen Ansatz),
hat dafür aber später die Möglichkeit eine Näherungslösung für 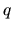 auf
auf
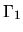 relativ einfach berechnen zu können.
Diese Eigenschaft kann beispielsweise bei der Berechnung elektrostatischer
Felder dazu genutzt werden, um die auf den Elektroden vorhandene Ladung zu
ermitteln, ohne dass dafür eigens der Gradient des Potenzials berechnet werden
muss.
relativ einfach berechnen zu können.
Diese Eigenschaft kann beispielsweise bei der Berechnung elektrostatischer
Felder dazu genutzt werden, um die auf den Elektroden vorhandene Ladung zu
ermitteln, ohne dass dafür eigens der Gradient des Potenzials berechnet werden
muss.
Im Folgenden werden die Gleichungen gemäß der Methode der gewichteten
Residuen für die
Feldberechnung in Isolatoren und Leitern, der Berechnung des transienten
elektrischen Feldes und der Wärmeleitungsgleichung angeschrieben.
Anmerkung zur Notation: Die Gleichungen werden nun speziell für das
elektrische Potenzial 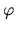 und die Temperatur
und die Temperatur 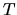 aufgestellt.
Anstelle der Materialkonstanten
aufgestellt.
Anstelle der Materialkonstanten
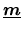 tritt entweder die
Permittivität
tritt entweder die
Permittivität
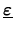 ,
die elektrische Leitfähigkeit
,
die elektrische Leitfähigkeit 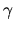 , bzw. die thermische
Leitfähigkeit
, bzw. die thermische
Leitfähigkeit 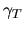 .
Bei Formeln mit allgemeiner Gültigkeit werden
weiterhin die Buchstaben
.
Bei Formeln mit allgemeiner Gültigkeit werden
weiterhin die Buchstaben 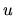 und
und
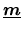 verwendet.
verwendet.
Für die Lösung der Gleichung des elektrischen Potenzials in anisotropen
Dielektrika (2.16)
mit den Randbedingungen (2.17) und (2.18) bzw.
allgemein mit (2.19)
erhält man die Koeffizienten 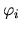 aus
aus
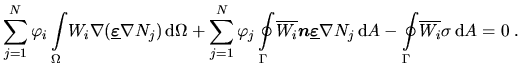 |
(4.22) |
Mit (4.12) (partielle Integration) und Gauß'schem Integralsatz
erhält man eine sogenannte schwache Form, mit reduzierter
Ordnung des Differentialoperators
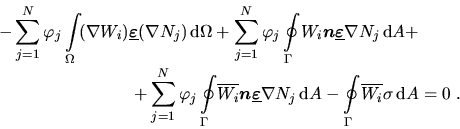 |
(4.23) |
Durch Wahl der Gewichtsfunktionen des Randresiduums mit
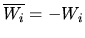 |
(4.24) |
verschwinden die beiden Randintegrale mit den Konormalableitungen.
Gemäß dem Galerkin-Verfahren werden die Gewichtsfunktionen den
Ansatzfunktionen gleichgesetzt
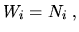 |
(4.25) |
wodurch sich (4.23) zu
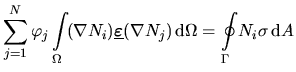 |
(4.26) |
vereinfacht.
Für die Ladungsverteilung 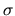 wird folgender Ansatz getroffen
wird folgender Ansatz getroffen
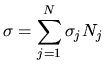 |
(4.27) |
und man erhält somit das Gleichungssystem
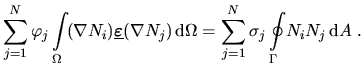 |
(4.28) |
Für die Berechnung der Potenzialverteilung in elektrischen Leitern
ist ebenfalls die Laplace-Gleichung (2.27)
mit den Randbedingungen (2.29) und (2.30)
zu lösen.
Hier wird völlig analog zum elektrostatischen Fall vorgegangen und
erhält zur Berechnung der unbekannten Koeffizienten 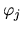 das
Gleichungssystem
das
Gleichungssystem
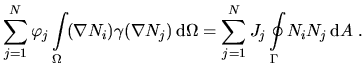 |
(4.29) |
Für die Berechnung des transienten Verhaltens des elektrischen Potenzials
gilt es (2.38) zu lösen, die auch folgendermaßen angeschrieben
werden kann:
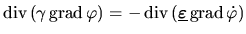 |
(4.30) |
wobei mit
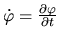 die Ableitung des Potenzials nach der
Zeit bezeichnet wird.
Die Randbedingungen lauten gemäß (2.17) und (2.39)
die Ableitung des Potenzials nach der
Zeit bezeichnet wird.
Die Randbedingungen lauten gemäß (2.17) und (2.39)
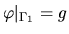 |
(4.31) |
und
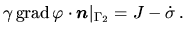 |
(4.32) |
Dabei soll die Ladungsdichte am Rand durch
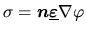 |
(4.33) |
ausgedrückt werden.
Mit dem Verfahren der gewichteten Residuen werden hier lediglich die
räumlichen Ableitungen des Differentialoperators diskretisiert--die
Zeit bleibt hier noch kontinuierlich.
Man erhält somit folgenden
Ansatz zur Berechnung der Näherungslösung
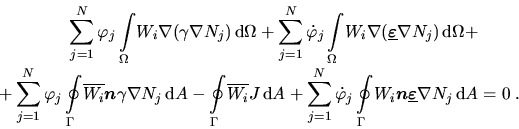 |
(4.34) |
Mittels partieller Integration erhält man wiederum die schwache Form
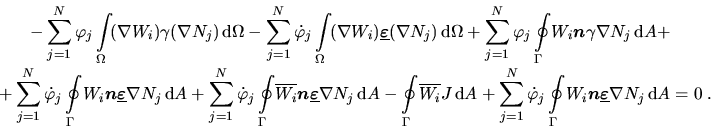 |
(4.35) |
Für die Gewichtsfunktionen am Rand wird wieder
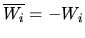 angenommen.
Weiters gilt gemäß dem Galerkin-Ansatz
angenommen.
Weiters gilt gemäß dem Galerkin-Ansatz 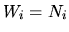 .
Für die Normalkomponente der Stromdichte am Rand wird die folgende
Näherung verwendet:
.
Für die Normalkomponente der Stromdichte am Rand wird die folgende
Näherung verwendet:
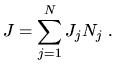 |
(4.36) |
Man erhält somit die folgende Gleichung zur Bestimmung der unbekannten
Koeffizienten:
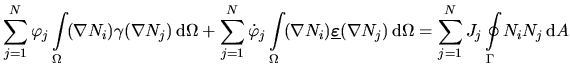 |
(4.37) |
Für die stationäre Wärmeleitungsgleichung (2.44)
mit den Randbedingungen (2.51) und (2.53)
wird
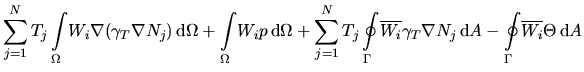 |
(4.38) |
Mittels schwacher Formulierung und Wahl der Gewichtsfunktionen analog
zu den elektrischen Systemen erhält man das Gleichungssystem
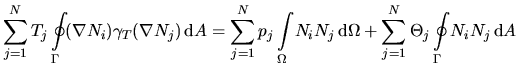 |
(4.39) |
Für die Lösung der transienten Wärmeleitungsgleichung (2.43)
mit den Randbedingungen wie in (2.51) und (2.53)
gilt analog
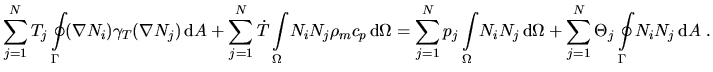 |
(4.40) |
Fußnoten
- ...
kommen.4.3
- Das Ritz'sche Verfahren und die Methode der gewichteten
Residuen mit Galerkin-Ansatz liefern für die hier behandelten partiellen
Differentialgleichungen exakt die gleiche Lösung.
Die Methode der gewichteten Residuen ist dabei das allgemeinere Verfahren,
mit dem zu jedem Variationsansatz eine äquivalente Formulierung
gefunden werden kann (aber nicht umgekehrt).



Next: 4.4 Elementformulierung
Up: 4. Diskretisierung mit Finiten
Previous: 4.2 Das Verfahren von
R. Sabelka: Dreidimensionale Finite Elemente Simulation von Verdrahtungsstrukturen auf Integrierten Schaltungen
![]() , sodass das Residuum
, sodass das Residuum
![]() zu wählen, denn von ihnen
hängt die Qualität der Lösung ab.
Z.B. werden bei der Methode der Kollokation Dirac-Impulse
zu wählen, denn von ihnen
hängt die Qualität der Lösung ab.
Z.B. werden bei der Methode der Kollokation Dirac-Impulse
![]() verwendet.
Eine andere gebräuchliche Methode ist es, die Testfunktionen den
Ansatzfunktionen gleichzusetzen
verwendet.
Eine andere gebräuchliche Methode ist es, die Testfunktionen den
Ansatzfunktionen gleichzusetzen ![]() . Diese Methode ist auch als
Galerkin-Ansatz bekannt und soll in dieser Arbeit zur Anwendung
kommen.4.3
. Diese Methode ist auch als
Galerkin-Ansatz bekannt und soll in dieser Arbeit zur Anwendung
kommen.4.3
![]() noch ein
Randresiduum
noch ein
Randresiduum ![]()
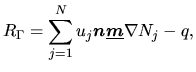
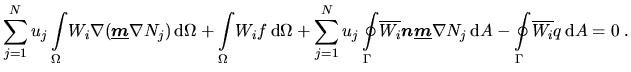
![]() und die Temperatur
und die Temperatur ![]() aufgestellt.
Anstelle der Materialkonstanten
aufgestellt.
Anstelle der Materialkonstanten
![]() tritt entweder die
Permittivität
tritt entweder die
Permittivität
![]() ,
die elektrische Leitfähigkeit
,
die elektrische Leitfähigkeit ![]() , bzw. die thermische
Leitfähigkeit
, bzw. die thermische
Leitfähigkeit ![]() .
Bei Formeln mit allgemeiner Gültigkeit werden
weiterhin die Buchstaben
.
Bei Formeln mit allgemeiner Gültigkeit werden
weiterhin die Buchstaben ![]() und
und
![]() verwendet.
verwendet.
![]() aus
aus
![]() das
Gleichungssystem
das
Gleichungssystem