next up previous contents
Next: 4. Simulation Models for Up: Dissertation Alireza Sheikholeslami Previous: 2. Mathematical Description of

Subsections


3. Topography Effects in Deposition and Etching

Fundamental physical mechanisms in deposition and etching processes generate both desired and undesired topographic features. In this chapter we provide a basis for understanding and modeling these effects on topography. A common framework for modeling etching and deposition is given, including the terminology used for describing the various physical phenomena and effects.

3.1 Common Aspects of Deposition and Etching

While deposition and etching are nearly opposites and there is great diversity of processing equipment used to perform them, from a topographical point of view they have a lot in common.

The starting point for both is the nature of flux which arrives from a source above the wafer. The second commonality is how the self-shadowing of an existing profile affects the visibility of the source and how the re-emission from the profile or radiosity affects other points of the profile. The third common aspect is that mechanical and chemical reactions at the surface determine the local advancement rate and are one of the most challenging aspects of deposition and etching. The final common characteristic of deposition and etching is the time-advance of the surface profile. In this chapter we focus on this final common aspect.

3.1.1 Flux Nature

In the case of deposition a broad angular distribution of small particles of target material is introduced from an upper electrode. In the case of etching there may be one or more positively charged species bombarding the wafer with a nearly vertical Gaussian distribution of incident angles.

Figure 3.1: An illustration of the boundary interaction with the incident flux and re-emission.
\includegraphics[width=0.5\linewidth]{shadowing}

Figure 3.2: A schematic of forming the protective layer on the side-walls during an anisotropic etching process.
\includegraphics[width=0.5\linewidth]{protective2}


3.1.2 Effects of Topography on the Visibility

The topography profile on the wafer affects the visibility of local points on the profile. Certain parts of the profile may cast shadows on other parts of the profile (cf. Figure 3.1) and thus reduce the visibility to various flux components. In deposition this plays a very important role in filling contacts with metal, because, as the aspect ratio of the contacts increases, it becomes increasingly difficult to deposit enough metal on either the bottom or the side-walls due to this shadowing. More complex point to point interactions along the topography profile can also be important. In deposition and etching processes a particle might not stick where it first lands, but plays a small game of billiards before coming to a final rest. This is known as re-emission (cf. Figure 3.1) and the sticking coefficient between zero and one is the fraction of the particles that sticks. A sticking coefficient of unity means that the particle sticks. Conversely, a low sticking coefficient means that the particle may bounce many times. In plasma etching and more properly reactive ion etching it is the directed flux of species, which passes through the mask opening that enhances the etch rate. The selectivity of the etch rate of the substrate relative to the mask has to be considered. High energy bombardment is associated with mechanical etching effects which are less selective than chemical etching. On the other hand the anisotropy of the etching can be enhanced by providing a thin protective layer mostly polymer on the side-walls (cf. Figure 3.2) against the spontaneous etch reaction. Indeed, this layer prevents lateral etching and then leads to the vertical side-walls during an etching process.

3.1.3 Surface Reaction

The third common aspect stems from mechanical and chemical reactions at the surface determining the local advancement rate. These are one of the most interesting phenomena of deposition and etching. In deposition, columnar grain growth is possible and the column angle tilts with the angle of incidence according to the billiard player's rule. In deposition and etching processes there is evidence that a specific orientation of the initial boundary can affect the final profile, because the shadowing effects due to visibility between the boundary and source plane depend on the orientation of the boundary relative to the source plane, i.e., it makes a difference when the boundary is aligned parallel or perpendicular to the source plane. Furthermore, surface mobility can introduce diffusion of species along the surface in both deposition and etching. In plasma etching the ion bombardment can both accelerate reactions and remove by-products. During etching a protective layer (cf. Section 3.1.2) can be formed that even protects from energetic neutrals and leads to vertical etch profiles [62].

3.1.4 Time-Advance of the Surface Profile

The local fluxes and etch or deposition reactions provide sufficient information on how the surface is to be deformed for a short time step. The time evolution of the profile requires many time increments which allow the change of the profile shape to influence its future shape through shadowing, etc. As the surface evolves there may be major topological changes. For example, outgrows of the material from sides of a trench might collide and close off a void, or etch fronts from two trenches might move laterally, collide and form a tunnel or an air bridge.

To ease the presentation a simpler two-dimensional case will be used. In two dimensions the profile is sometimes said to be made of line segments and intersections points which may also be called nodes. Figure 3.3 shows the simulation result of an isotropic deposition of a material into a rectangular structure. It can be seen easily that the boundary is expanded radially outward for a time step $ \Delta t=t_{2}-t_{1}$. The top right convex outward corner point causes a fan (cf. Figure 3.3) of facets to be generated which creates a rounded section in the profile at time $ t_{2}$. At the concave outward corner the planar fronts from the horizontal and vertical facets intersect in a line which is the location of a new corner point. These collisions where overlapping fronts occur and some information about the initial profile is lost are said to be shocks (cf. Figure 3.3). Note that shocks and fans play a very important role in determining the changes of topography during processing. For isotropic etching the profile moves from the surface into the material as shown in Figure 3.4. As expected the convex outward corner now produces a shock and the concave corner point produces a fan.

Figure 3.3: Isotropic deposition of a material into a rectangular structure.



\includegraphics[width=0.8\linewidth]{figures/faceting-deposition2}
Figure 3.4: Isotropic etching of a material from a rectangular structure.




\includegraphics[width=0.8\linewidth]{figures/faceting-etching}
Figure 3.5: Geometry for the analysis of the advancement of the intersection between two adjacent facets.
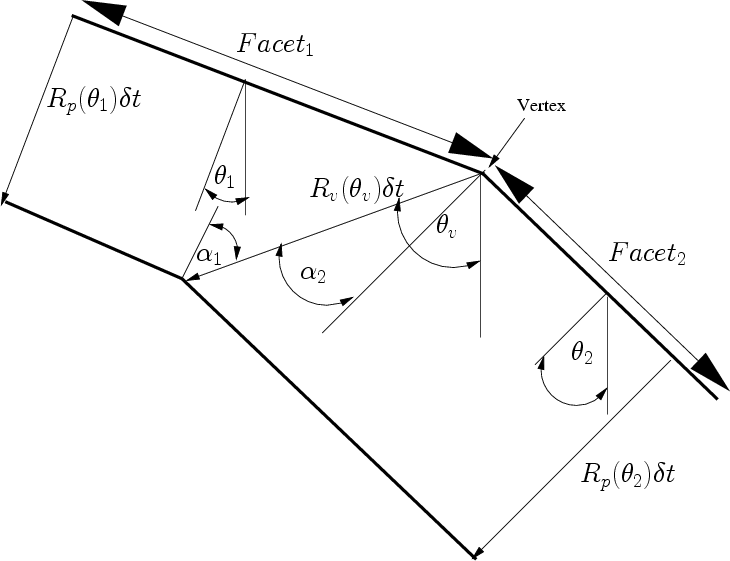\begin{figure}\vspace*{1.5cm} \input{test.pstex_t}\end{figure}

3.1.5 Basic Facet Analysis

To understand faceting of the initial profile the advancement of two neighboring facets as shown in Figure 3.5 is considered. The direction and rate of advance of a vertex where two facets intersect is of key interest. The two facets have downward normals which form angles $ \theta_{1}$ and $ \theta_{2}$ with respect to the vertical downward direction. They advance a distance which is the product of the planar etch rate for their orientation $ R_{p}(\theta)$ and time step $ \delta t$ as $ R_{p}(\theta_{1})\delta t$ and $ R_{p}(\theta_{2})\delta t$, respectively. The vertex moves at an angle $ \theta_{v}$ and a rate $ R_{v}(\theta_{v})$ and therefore a distance $ R_{v}(\theta_{v})\delta t$. The angles of the path of this vertex with respect to the normal of the two facets are $ \alpha_{1}$ and $ \alpha_{2}$ which are $ \theta_{v}-\theta_{1}$ and $ \theta_{v}-\theta_{2}$, respectively. Projecting the distance of movement of this vertex onto the distances advanced by the facets gives the two following equations:

$\displaystyle R_{v}(\theta_{v})\delta t\cos(\theta_{v}-\theta_{1})= R_{p}(\theta_{1})\delta t$ (3.1)

$\displaystyle R_{v}(\theta_{v})\delta t\cos(\theta_{v}-\theta_{2})= R_{p}(\theta_{2})\delta t$ (3.2)

Taking the ratio between (3.1) and (3.2) and eliminating $ R_{v}(\theta_{v})$ gives

$\displaystyle \frac{\cos(\theta_{2}-\theta_{v})}{\cos(\theta_{1}-\theta_{v})}=\frac{R_{p}(\theta_{2})}{R_{p}(\theta_{1})}.$ (3.3)

Once $ \theta_{v}$ is known the associated rate $ R_{v}(\theta_{v})$ can be found from (3.1) and (3.2) and is of course higher than $ R_{p}(\theta_{1})$ and $ R_{p}(\theta_{2})$.

(3.3) makes a number of interesting predictions about the physical nature of the motion of the vertex. Assuming that $ \theta_{1}<\theta_{v}<\theta_{2}$ and $ R_{p}$ is not a function of the facet angle $ \theta$, then the right hand side of (3.3) is unity, forcing $ \theta_{2}-\theta_{v}=\theta_{v}-\theta_{1}$ or $ \theta_{v}=\theta_{1}+\theta_{2}/2$ which means that the intersection vertex moves along the bisecting angle.

Another important case is that $ R_{p}$ increases with the angle $ \theta$. This makes the right hand side of (3.3)$ >1$ which leads to $ \theta_{2}-\theta_{v}<\theta_{v}-\theta_{1}$ or $ \theta_{v}>\theta_{1}+\theta_{2}/2$. This means that the faster moving facet will encroach into the region of the slower moving facet and likely expands in size.

To further explore how the movement of a facet depends on the shape of the rate function, the direction of travel of a facet at angle $ \theta$ with rate function $ R_{\theta}$ is now derived in a limiting case. Assuming that the angle between a facet pair is small enough, their intersection vertex will propagate in the direction of motion of the facet. This limiting case can be determined from (3.3) by taking the special case of $ \theta_{1}=\theta$ and $ \theta_{2}=\theta+\delta\theta$ and letting $ \delta\theta$ go to zero. Substituting $ \theta_{1}$ and $ \theta_{2}$ in (3.3) and expanding $ R_{p}$ in a Taylor series gives

$\displaystyle \cos(\delta\theta)-\frac{\sin(\theta-\theta_{v})\sin(\delta\theta... ...eta)}=1+\frac{d R_{p}(\theta)}{d\theta}\cdot\frac{\delta\theta}{R_{p}(\theta)}.$ (3.4)

Letting $ \delta\theta$ go to zero in (3.4) gives

$\displaystyle \tan(\theta_{v}-\theta)=\frac{d R_{p}(\theta)}{d\theta}\cdot \frac{1}{R_{p}(\theta)}.$ (3.5)

(3.5) indicates that a facet at angle $ \theta$ moves laterally with a rate component proportional to the slope of the rate function $ d R_{p}(\theta)/d\theta$ as well as normal to the surface at the usual rate $ R_{p}(\theta)$.


3.1.6 Corner Rounding

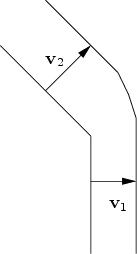
Regarding the evolution of facets each facet has a plane associated with it. The plane moves with a given normal speed which may be different for different facets. The boundaries of the facets are determined by the intersection of the planes. The two-dimensional evolution near a corner is shown in Figure 3.6. If we use a level-set method where the normal speed is a simple interpolation between the two normal speeds, then the corners would be rounded, as shown in Figure 3.7 (in particular, an arc of a circle would arise, if the two speeds are the same). In order to keep flat facets and sharp corners, the following precautions must be made. The evolution of a smooth curve only depends on the normal speed, the addition of a tangential component only has the effect of changing the parameterization of the curve. With a velocity that has a proper tangential component to the facet and is directed towards a corner, the facets will evolve maintaining sharp

Figure 3.6: Facet evolution near a corner.
\begin{figure}\hspace*{4.5cm} \input{facet.pstex_t}\end{figure}
Figure 3.7: Evolution near a corner when the normal speed at the corner is a linear interpolation of the normal speeds of the two facets.
\begin{figure}\hspace*{5.5cm} \input{facetrounded.pstex_t}\end{figure}
corners as shown in Figure 3.6. For example, for $ \mathbf{v}_{1}=\mathbf{v}_{2}$ and a square corner, the necessary tangential velocity component which has to be added on both sides of the corner is $ \mathbf{v}_{1}$. Note that this is a lower bound for the tangential velocity. In fact, if we move the points with a tangential velocity larger than this value, the evolution of the interface will still be the same. The addition of the tangential velocity causes the characteristics to collide; the solution does not become multivalued, because standard techniques are used for viscosity solutions of the Hamilton-Jacobi equation [71]. This causes a shock to form and maintains a sharp corner. Note that the velocity that we add is tangential to the facet, not to the interface. This has the effect of modifying the normal component of the interface, if the latter is not aligned with the facet. In this respect the method can be viewed as a technique to construct a proper normal velocity law, given the speeds of the facets.
Figure 3.8: Geometry to analyze the advancement of the intersection between two adjacent facets.
\begin{figure}\hspace*{3.5cm} \input{corner.pstex_t}\end{figure}


3.2 Minimizing the Corner Rounding

In order to minimize the corner rounding during the movement of a boundary the approach introduced by Russo and Smereka [71] can be used where the speed of each facet must be specified. Consider an interface consisting of $ M$ facets, with normals $ \mathbf{v}_{m}$ and absolute value of normal speeds $ \omega_{m}$ for $ m=1,...,M$. Let $ \mathbf{n}$ be the normal at a given point of the interface.

In order to compute the proper velocity of the surface at a given point, first the facet is selected which is closest in direction to $ \mathbf{n}$, i.e., for which $ n \cdot \mathbf{v}_{m}$ is a maximum,

$\displaystyle k=\mathrm{arg max}_{m}(\mathbf{n}\cdot \mathbf{v}_{m}).$ (3.6)

Next the following velocity is defined

$\displaystyle \mathbf{c}=\omega_{k}\mathbf{n}+u\mathbf{a}$ (3.7)

where

$\displaystyle \mathbf{a}=\frac{\mathbf{n}-(\mathbf{n}\cdot\mathbf{v}_{k})\mathb... ...{n}\cdot\mathbf{v}_{k})\mathbf{v}_{k}\vert^{2}+\varepsilon ^{2}]^{\frac{1}{2}}}$ (3.8)

and $ u$ is the tangential speed which will be specified below. The parameter $ \varepsilon $ in the denominator is a numerical parameter which ensures that $ \mathbf{a}$ vanishes smoothly when the numerator vanishes.

Some simple geometric considerations as shown in Figure 3.8 and the following equations help us to find the tangential speed that must be added to keep a sharp corner.

$\displaystyle (\omega_{1}+u^{\perp}_{12}\tan\alpha)^{2}+\omega_{2}^{2}-2\omega_{2}(\omega_{1}+u^{\perp}_{12}\tan\alpha)\cos\alpha=d^{2}$ (3.9)

where $ d=l\cos\alpha$ and $ l=(\omega_{1}+u^{\perp}_{12}\tan\alpha)\tan\alpha$. Substituting $ l$ and $ d$ in (3.9) gives

$\displaystyle [(\omega_{1}+u^{\perp}_{12}\tan\alpha)\cos\alpha-\omega_{2}]^{2}=0$ (3.10)

and finally the equation for the tangential speed is as follows:

$\displaystyle u^{\perp}_{12}=\frac{\omega_{2}-\omega_{1}\cos\alpha}{\sin\alpha}$ (3.11)

The quantity $ u$ can then be chosen equal to $ u^{*}$, where

$\displaystyle u^{*}=\mathrm{max}_{ij}u^{\perp}_{ij}$ (3.12)

where facet $ i$ is a neighbor of facet $ j$ and $ \omega_{j}\ge\omega_{i}$.

For a faceted interface $ \mathbf{a}=0$, because $ \mathbf{n}=\mathbf{v}_{k}$ and the facet will evolve with the standard normal speed. On the other hand, if we evolve the whole interface with the velocity $ \mathbf{v}=\omega_{k}\mathbf{n}$, then the corners get rounded as shown in Figure 3.7. When the corners become slightly rounded, then $ \mathbf{a}$ becomes directed towards the corners and the surface will move with a velocity that will try to keep the corners sharp.

Choosing a small value for $ \varepsilon $, the vector $ \mathbf{a}$ is basically a unit vector whenever $ \mathbf{n}$ is not aligned with the facets. Neglecting $ \varepsilon $, the normal speed $ \mathbf{c}$ can be calculated from (3.7) with the following equation

$\displaystyle \mathbf{c}^{\perp}=\omega_{k}\mathbf{n}+u\mathbf{a}^{\perp}$ (3.13)

The normal part of $ \mathbf{a}$ can be calculated from (3.8) as follows:

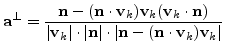$\displaystyle \mathbf{a}^{\perp}= \frac{\mathbf{n}- (\mathbf{n}\cdot\mathbf{v}_... ...\vert\cdot \vert\mathbf{n}-(\mathbf{n}\cdot \mathbf{v}_{k})\mathbf{v}_{k}\vert}$ (3.14)

and therefore

$\displaystyle \vert\mathbf{a}^{\perp}\vert=\frac{1-(\mathbf{n}\cdot\mathbf{v}_{... ...t{1+(\mathbf{n}\cdot\mathbf{v}_{k})^{2}-2(\mathbf{n}\cdot\mathbf{v}_{k})^{2}}}.$ (3.15)

Substituting (3.15) in (3.13) gives the normal speed of our model for the level set function

$\displaystyle F=\omega_{k}+u\sqrt{1-(\mathbf{n}\cdot\mathbf{v}_{k})^{2}}.$ (3.16)

In Chapter 7 we will present the application of this method to get the trenches with a minimal corner rounding during the simulation of an etching process.

next up previous contents
Next: 4. Simulation Models for Up: Dissertation Alireza Sheikholeslami Previous: 2. Mathematical Description of
A. Sheikholeslami: Topography Simulation of Deposition and Etching Processes