6.4 FEM Calculations of Residual Stress in Single Droplets
Seel developed a FEM approach for the encounter of two islands discussed in the
previous section [98][99]. He posed the problem in the same manner as Nix and
Clemens and from his simulations he calculated a height 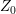 , which minimizes the
coalescence energy. By doing so, he imposed a series of displacements in both
droplets’ surfaces toward the center and computed the coalescence height which
minimizes the energy per unit length of the island surfaces. A sketch is shown in
Fig. 6.8.
, which minimizes the
coalescence energy. By doing so, he imposed a series of displacements in both
droplets’ surfaces toward the center and computed the coalescence height which
minimizes the energy per unit length of the island surfaces. A sketch is shown in
Fig. 6.8.
A semi-analytical solution for 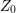 was also developed in Seel’s work. He took an
approach similar to Hoffman, but instead of assuming free energy conservation, he
considered the total energy per unit length of the island interfaces, which is given
by
was also developed in Seel’s work. He took an
approach similar to Hoffman, but instead of assuming free energy conservation, he
considered the total energy per unit length of the island interfaces, which is given
by
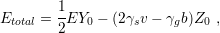 | (6.8) |
where ](diss525x.png) . The first term is the elastic energy which Seel
obtained by fitting the FEM results in different contact angles. As in the Hoffman model,
the second term represents the available energy after the creation of grain boundaries. In
contrast to Hoffman’s model, Seel’s analysis does not require energy conservation, because
the analysis is restricted to the interface of the islands. However, if the entire system is
considered, the energy must be obviously conserved.
. The first term is the elastic energy which Seel
obtained by fitting the FEM results in different contact angles. As in the Hoffman model,
the second term represents the available energy after the creation of grain boundaries. In
contrast to Hoffman’s model, Seel’s analysis does not require energy conservation, because
the analysis is restricted to the interface of the islands. However, if the entire system is
considered, the energy must be obviously conserved.
The minimum energy point defines the coalescence height 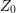 . Although it is possible to
obtain an analytical solution for
. Although it is possible to
obtain an analytical solution for 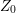 from (6.8) (
from (6.8) (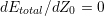 ), it is very cumbersome
and a numerical treatment is preferable. Seel’s approach is very flexible, presents results
similar to the Freund-Chason model with a slight tendency for underestimation, and is very
suitable for engineering purposes.
), it is very cumbersome
and a numerical treatment is preferable. Seel’s approach is very flexible, presents results
similar to the Freund-Chason model with a slight tendency for underestimation, and is very
suitable for engineering purposes.
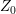 , which minimizes the
coalescence energy. By doing so, he imposed a series of displacements in both
droplets’ surfaces toward the center and computed the coalescence height which
minimizes the energy per unit length of the island surfaces. A sketch is shown in
Fig. 6.8.
, which minimizes the
coalescence energy. By doing so, he imposed a series of displacements in both
droplets’ surfaces toward the center and computed the coalescence height which
minimizes the energy per unit length of the island surfaces. A sketch is shown in
Fig. 6.8.
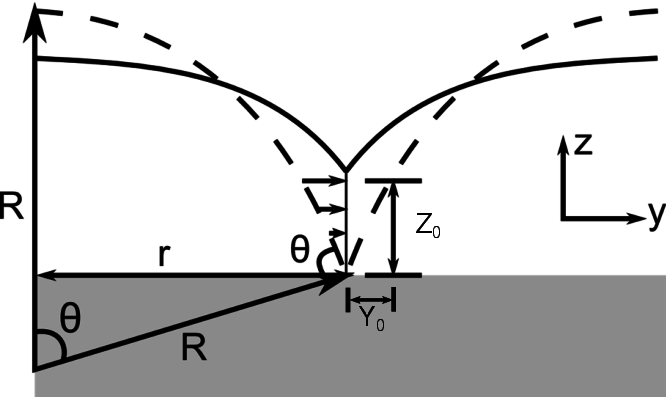
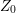 and the surface is displaced at most by
and the surface is displaced at most by 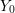 . The angle formed
between the droplet and the deposition substrate is identified by
. The angle formed
between the droplet and the deposition substrate is identified by 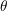 . Image based on
. Image based on
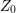 was also developed in Seel’s work. He took an
approach similar to Hoffman, but instead of assuming free energy conservation, he
considered the total energy per unit length of the island interfaces, which is given
by
was also developed in Seel’s work. He took an
approach similar to Hoffman, but instead of assuming free energy conservation, he
considered the total energy per unit length of the island interfaces, which is given
by
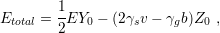
](diss525x.png) . The first term is the elastic energy which Seel
obtained by fitting the FEM results in different contact angles. As in the Hoffman model,
the second term represents the available energy after the creation of grain boundaries. In
contrast to Hoffman’s model, Seel’s analysis does not require energy conservation, because
the analysis is restricted to the interface of the islands. However, if the entire system is
considered, the energy must be obviously conserved.
. The first term is the elastic energy which Seel
obtained by fitting the FEM results in different contact angles. As in the Hoffman model,
the second term represents the available energy after the creation of grain boundaries. In
contrast to Hoffman’s model, Seel’s analysis does not require energy conservation, because
the analysis is restricted to the interface of the islands. However, if the entire system is
considered, the energy must be obviously conserved.
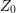 . Although it is possible to
obtain an analytical solution for
. Although it is possible to
obtain an analytical solution for 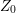 from (
from (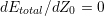 ), it is very cumbersome
and a numerical treatment is preferable. Seel’s approach is very flexible, presents results
similar to the Freund-Chason model with a slight tendency for underestimation, and is very
suitable for engineering purposes.
), it is very cumbersome
and a numerical treatment is preferable. Seel’s approach is very flexible, presents results
similar to the Freund-Chason model with a slight tendency for underestimation, and is very
suitable for engineering purposes.