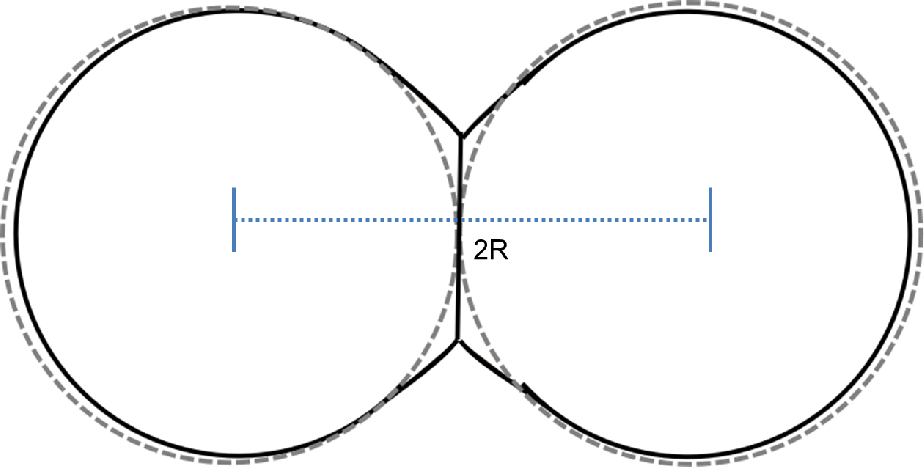
| Figure 6.7.: | Freund-chason model. |
Freund and Chason took a completely different approach for the islands’ encounter [107]. They treated the problem using the Hertzian contact theory with cohesive attraction [108], in an attempt to overcome the deficiencies in the description of the zipping process by Nix and Clemens. The geometry of the problem was also changed; in fact, they claim that the conditions in the Nix-Clemens model are suitable in the case of a fully covered substrate while the depositing material is only filling gaps. Therefore, Freund and Chason proposed a change in the perspective of the problem. Instead of using a transversal cross section, they decided to analyze the process using a top view of the structure, as shown in Fig. 6.7.
In fact, the Freund-Chason model expands the dimensionality of the problem and a 3D description of the geometry is also possible. The stress estimation using the Freund-Chason model is given by
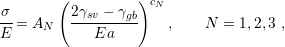 | (6.7) |
where 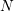 is the problem dimensionality.
is the problem dimensionality. 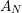 and
and 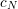 are parameters which
depend on the stated problem dimension with values
are parameters which
depend on the stated problem dimension with values 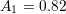 ,
, 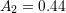 ,
,
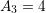 , and
, and 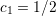 ,
, 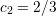 ,
, 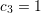 . The Freund-Chason model is more in
line with experimental measurements, especially for materials with high adatom
mobility.
. The Freund-Chason model is more in
line with experimental measurements, especially for materials with high adatom
mobility.