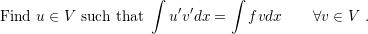
The Galerkin method was developed by the mathematicians Boris Galerkin and Walther Ritz (separately) to treat variational problems similar to (3.4) [56][57][58]. In fact, Galerkin attempted to solve a restricted version of (3.4) as described by
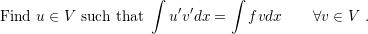 | (3.5) |
The constraints of the solution  to the same space of the test function (
to the same space of the test function (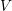 ) is very
convenient, as it will be shown in the end of Section 3.1.5, but the central question right
now is, if the solution
) is very
convenient, as it will be shown in the end of Section 3.1.5, but the central question right
now is, if the solution  of (3.5) still satisfies the original PDE, (3.1). In order to prove
that it does, a good strategy is to derive (3.1) from (3.5). Hence, let
of (3.5) still satisfies the original PDE, (3.1). In order to prove
that it does, a good strategy is to derive (3.1) from (3.5). Hence, let  be the solution of
(3.5), then it follows that (3.6) must also be satisfied
be the solution of
(3.5), then it follows that (3.6) must also be satisfied
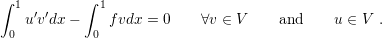 | (3.6) |
In addition to the restrictions imposed on  , consider that
, consider that 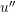 exists and is continuous.
Integrating the first term by parts and using the boundary conditions (v(0) = v(1) = 0) the
following relation holds
exists and is continuous.
Integrating the first term by parts and using the boundary conditions (v(0) = v(1) = 0) the
following relation holds
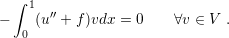 | (3.7) |
Since  is continuous, (3.7) can only stand, if the following relation is true
[56]
is continuous, (3.7) can only stand, if the following relation is true
[56]
![(u ′′ + f)(x) = 0,x ∈ [0,1] .](diss237x.png) | (3.8) |
Consequently,  satisfies the original BVP (3.1). However, it was necessary to assume
satisfies the original BVP (3.1). However, it was necessary to assume  as a well behaved function (second differentiable continuous). This restriction should satisfy
most physical problems, but attention must be paid for careless application of Galerkin’s
method.
as a well behaved function (second differentiable continuous). This restriction should satisfy
most physical problems, but attention must be paid for careless application of Galerkin’s
method.
So far only the equivalence of the solution between Galerkin’s problem and (3.1) was
discussed, but not the method itself. Galerkin’s method is developed upon the
discretization of (3.6) based on the discretization of the space  as presented in the next
section.
as presented in the next
section.