3.1.6 Final Remarks on FEM
The Finite Element Method is a vast and still very active subject of research. This text is
not intended to discuss it exhaustively, but to give a first intuitive approach and still formal
enough to understand this work. However, some points are still open, for instance, an
understanding of the conditions under which the FEM converges is still needed. As
mentioned previously, one expects that the discretized solution (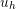 ) converges to the exact
solution (
) converges to the exact
solution ( ) by increasing the
) by increasing the 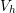 space dimension – in other words, increasing the
number of mesh points. Actually, this discussion leads to restrictions of the basis functions
to ensure FEM convergence (and also stability) [56][59]. An in-depth treatment about this
topic can be found in specific functional analysis texts, as well as in FEM books
[56][57][59].
space dimension – in other words, increasing the
number of mesh points. Actually, this discussion leads to restrictions of the basis functions
to ensure FEM convergence (and also stability) [56][59]. An in-depth treatment about this
topic can be found in specific functional analysis texts, as well as in FEM books
[56][57][59].
Another point of contention is the boundary conditions. In the previous sections, only
specific Dirichlet boundary conditions [61] were discussed. Indeed, for general
Dirichlet conditions all the previous results remain unchanged, less a constant, but for
Neumann boundary conditions [61] a new development is needed, especially for
the equivalence between the BVP problem and the variational formulation. The
procedure for deriving FEM is still the same, as well as the conclusions, but the
arguments must be modified to include this kind of situation. A self-contained text
about this subject can be found in traditional FEM references [56]; in addition,
an example with a Neumann boundary condition will be provided in the next
section.
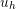 ) converges to the exact
solution (
) converges to the exact
solution ( ) by increasing the
) by increasing the 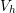 space dimension – in other words, increasing the
number of mesh points. Actually, this discussion leads to restrictions of the basis functions
to ensure FEM convergence (and also stability) [56][59]. An in-depth treatment about this
topic can be found in specific functional analysis texts, as well as in FEM books
[56][57][59].
space dimension – in other words, increasing the
number of mesh points. Actually, this discussion leads to restrictions of the basis functions
to ensure FEM convergence (and also stability) [56][59]. An in-depth treatment about this
topic can be found in specific functional analysis texts, as well as in FEM books
[56][57][59].