2.1.1 Spannungsfestigkeit




Next: 2.1.2 Die Kontaktierung des
Up: 2.1 DMOS-Grundstrukturen
Previous: 2.1 DMOS-Grundstrukturen
Das niedrig dotierte 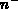 -Substrat dient als sog. Driftzone, die hohe
Drainspannungen aufnehmen kann. Mit dieser Dotierung ist ein
verhältnismäßig hoher Widerstand verbunden, der bei Stromfluß einen
Großteil der Drain-Source-Spannung aufnimmt, sodaß am Kanal selbst nur ein
Bruchteil dieser Spannung abfällt.
-Substrat dient als sog. Driftzone, die hohe
Drainspannungen aufnehmen kann. Mit dieser Dotierung ist ein
verhältnismäßig hoher Widerstand verbunden, der bei Stromfluß einen
Großteil der Drain-Source-Spannung aufnimmt, sodaß am Kanal selbst nur ein
Bruchteil dieser Spannung abfällt.
Im stromlosen Fall ist (bei 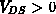 ) der
) der  -Übergang zwischen
-Übergang zwischen
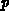 -body und Driftgebiet gesperrt. Es bildet sich eine
Raumladungszone, die die Drain-Source-Spannung aufnehmen muß. Eine
Raumladungszone um einen
-body und Driftgebiet gesperrt. Es bildet sich eine
Raumladungszone, die die Drain-Source-Spannung aufnehmen muß. Eine
Raumladungszone um einen  -Übergang dehnt sich weiter in jenen Bereich
aus, der niedriger dotiert ist. Dies kann sehr einfach über die Lösung der
eindimensionalen Poissongleichung gezeigt werden, die (mit dem
elektrostatischen Potential
-Übergang dehnt sich weiter in jenen Bereich
aus, der niedriger dotiert ist. Dies kann sehr einfach über die Lösung der
eindimensionalen Poissongleichung gezeigt werden, die (mit dem
elektrostatischen Potential 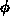 , dem elektrischen Feld
, dem elektrischen Feld 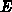 in
in
 -Richtung, der Raumladung
-Richtung, der Raumladung 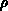 zufolge der ionisierten
Akzeptor- und Donatorkonzentrationen
zufolge der ionisierten
Akzeptor- und Donatorkonzentrationen 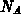 und
und 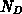 in der Raumladungszone)
lautet:
in der Raumladungszone)
lautet:
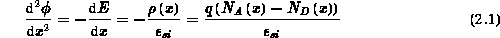
Für einen abrupten  -Übergang an der Stelle
-Übergang an der Stelle 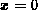 mit
mit
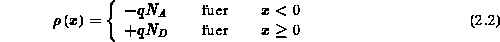
ergibt sich für die Grenzen der Raumladungszone in 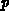 - und
- und  -Gebiet:
-Gebiet:
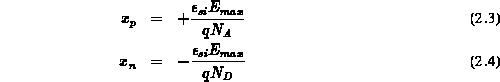
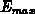 ist negativ und folgt mit der in Sperrichtung angelegten
Spannung
ist negativ und folgt mit der in Sperrichtung angelegten
Spannung 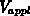 zu:
zu:
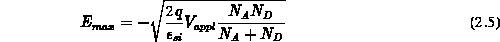
Auf nicht abrupt, sondern z.B. linear verlaufende  -Übergänge lassen
sich die folgenden Überlegungen gleichermaßen anwenden (siehe
z.B. [116]). Man sieht aus den Gleichungen 2.3 und
2.4, daß sich das Verarmungsgebiet immer in das niedriger
dotierte Gebiet weiter ausdehnt. Bei stark unterschiedlicher Dotierung auf
beiden Seiten des
-Übergänge lassen
sich die folgenden Überlegungen gleichermaßen anwenden (siehe
z.B. [116]). Man sieht aus den Gleichungen 2.3 und
2.4, daß sich das Verarmungsgebiet immer in das niedriger
dotierte Gebiet weiter ausdehnt. Bei stark unterschiedlicher Dotierung auf
beiden Seiten des  -Übergangs dehnt sich die Raumladungszone praktisch
ausschließlich in das niedrig dotierte Gebiet aus. Auch ist die maximale
Feldstärke
-Übergangs dehnt sich die Raumladungszone praktisch
ausschließlich in das niedrig dotierte Gebiet aus. Auch ist die maximale
Feldstärke 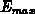 in diesem Fall lediglich durch das niedrig dotierte
Gebiet bestimmt (siehe Gleichung 2.5 für
in diesem Fall lediglich durch das niedrig dotierte
Gebiet bestimmt (siehe Gleichung 2.5 für 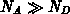 oder
umgekehrt). Je niedriger dieses dotiert ist, desto geringer ist die maximale
Feldstärke (sie tritt immer im metallurgischen
oder
umgekehrt). Je niedriger dieses dotiert ist, desto geringer ist die maximale
Feldstärke (sie tritt immer im metallurgischen  -Übergang, also in
unserem Beispiel bei
-Übergang, also in
unserem Beispiel bei 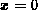 auf).
auf).
Geht man davon aus, daß die Driftzone in einem DMOS-Transistor wesentlich
weniger stark dotiert ist als der 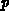 -body, so muß die Driftzone weit
genug sein, sodaß im Vorwärts-Sperrfall die Raumladungszone nicht das hoch
dotierte Draingebiet erreicht, da sie sich sonst nicht mehr weiter
ausdehnen kann. Mit steigender Spannung wächst die Feldstärke stark an
und bedingt einen früheren Lawinendurchbruch [3]. Auf der anderen
Seite dringt natürlich die Verarmungszone auch etwas in den
-body, so muß die Driftzone weit
genug sein, sodaß im Vorwärts-Sperrfall die Raumladungszone nicht das hoch
dotierte Draingebiet erreicht, da sie sich sonst nicht mehr weiter
ausdehnen kann. Mit steigender Spannung wächst die Feldstärke stark an
und bedingt einen früheren Lawinendurchbruch [3]. Auf der anderen
Seite dringt natürlich die Verarmungszone auch etwas in den 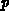 -body
ein. Durch das Design muß sichergestellt sein, daß diese nicht das
-body
ein. Durch das Design muß sichergestellt sein, daß diese nicht das
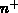 -Sourcegebiet erreicht, da es sonst zum sog. punch
through-Durchbruch kommt.
-Sourcegebiet erreicht, da es sonst zum sog. punch
through-Durchbruch kommt.
DMOS-Transistoren sind i.a. so ausgelegt, daß es zu keinen
punch through-Problemen kommt. Die Vorwärts-Blockiereigenschaften
werden damit durch den Lawinendurchbruchsmechanismus an gesperrten
 -Übergängen begrenzt. Als Näherungsformel für die Durchbruchspannung
eines ebenen, abrupten
-Übergängen begrenzt. Als Näherungsformel für die Durchbruchspannung
eines ebenen, abrupten  -Übergangs für
-Übergangs für 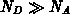 wird in
[8] angegeben:
wird in
[8] angegeben:
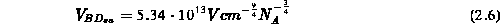
Die Weite der Raumladungszone ergibt sich zu:
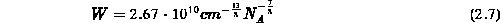
Abb. 2.2 zeigt diese Zusammenhänge graphisch:
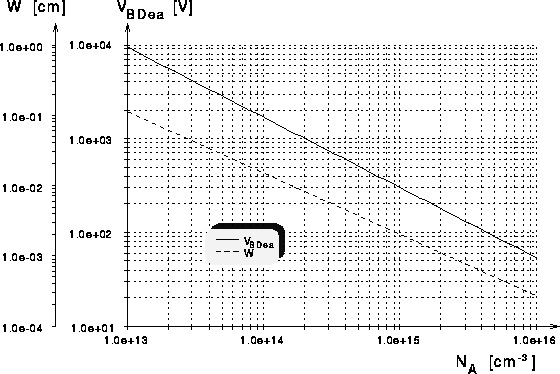
Abbildung 2.2: Durchbruchspannung und Weite eines
ebenen, abrupten  -Übergangs über der Konzentration des geringer
dotierten Gebiets.
-Übergangs über der Konzentration des geringer
dotierten Gebiets.
In einer realen DMOS-Struktur treten Krümmungen der Raumladungszonen auf,
die Feldstärkespitzen verursachen. Abb. 2.3 läßt vermuten, daß
diese umso stärker sind, je größer das Verhältnis der Weite der
Raumladungszone zum Krümmungsradius des  -Übergangs ist.
-Übergangs ist.
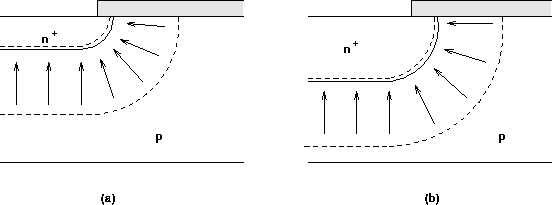
Abbildung 2.3: Feldverlauf am Rand eines
seichten (a) und eines tiefen (b)  -Übergangs.
-Übergangs.
Geht man von einer zweidimensionalen Struktur mit abrupten, zylindrischen
Übergängen aus (unter der vereinfachenden Annahme, daß die laterale
Unterdiffusion der Tiefe des  -Übergangs entspricht), so führt eine
Berechnung über die Lösung der
Poissongleichung in Zylinderkoordinaten zu folgender Durchbruchspannung
(
-Übergangs entspricht), so führt eine
Berechnung über die Lösung der
Poissongleichung in Zylinderkoordinaten zu folgender Durchbruchspannung
( ist der Radius des
ist der Radius des  -Übergangs) [7][10]:
-Übergangs) [7][10]:
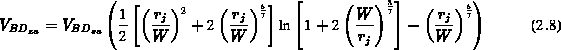
Ein reale, dreidimensionale Struktur weist jedoch an ihren Ecken Übergänge
auf, die durch das Aufeinandertreffen von zwei zylindrischen
 -Übergängen im Winkel von i.a.
-Übergängen im Winkel von i.a. 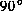 entstehen. Für einen
abrupten, sphärischen Übergang kann die Poissongleichung in
Kugelkoordinaten gelöst werden. Die Durchbruchspannung ergibt sich im
Vergleich zu der eines ebenen, abrupten Übergangs
zu [7][10]:
entstehen. Für einen
abrupten, sphärischen Übergang kann die Poissongleichung in
Kugelkoordinaten gelöst werden. Die Durchbruchspannung ergibt sich im
Vergleich zu der eines ebenen, abrupten Übergangs
zu [7][10]:
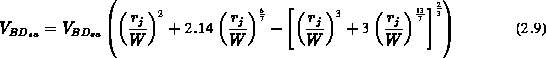
Die Gleichungen 2.8 und 2.9 gelten für 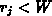 und
für eine Hintergrunddotierung kleiner als
und
für eine Hintergrunddotierung kleiner als 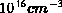 (ein sehr hoher
Wert für die Grunddotierung).
Abb. 2.4 zeigt die auf die Durchbruchspannung des abrupten,
ebenen
(ein sehr hoher
Wert für die Grunddotierung).
Abb. 2.4 zeigt die auf die Durchbruchspannung des abrupten,
ebenen  -Übergangs normierten Durchbruchspannungen der
zylindrischen und sphärischen Übergänge. Man erkennt, daß die
Durchbruchspannung mit kleiner werdendem Radius des
-Übergangs normierten Durchbruchspannungen der
zylindrischen und sphärischen Übergänge. Man erkennt, daß die
Durchbruchspannung mit kleiner werdendem Radius des
 -Übergangs sinkt. Wie zu erwarten war, ist die Durchbruchspannung des
sphärischen Übergangs deutlich niedriger als die des zylindrischen.
-Übergangs sinkt. Wie zu erwarten war, ist die Durchbruchspannung des
sphärischen Übergangs deutlich niedriger als die des zylindrischen.
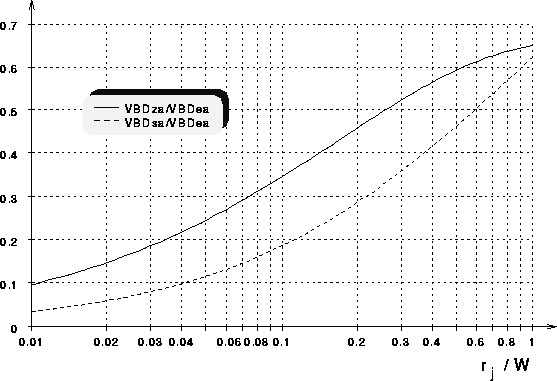
Abbildung 2.4: Durchbruchspannungen von zylindrischen und sphaerischen, abrupten  -Uebergaengen im Verhaeltnis zu ebenen, abrupten
-Uebergaengen im Verhaeltnis zu ebenen, abrupten
 -Uebergaengen.
-Uebergaengen.
Es zeigt sich auch (wie schon aus Abb. 2.3 zu vermuten), daß das
Verhältnis von Krümmungsradius zur Weite des  -Übergangs eine
wesentliche Größe ist. Sehr seichte
-Übergangs eine
wesentliche Größe ist. Sehr seichte  -Übergänge bedingen kleine
Radien und
verringern die Durchbruchspannung. Für Leistungsbauelemente sind daher oft
zusätzliche Prozeßschritte (Diffusionen) notwendig, um tiefere Übergänge
zu erzielen. Da sphärische Übergänge durch Aufeinandertreffen von
zylindrischen Übergängen an Ecken der Struktur hervorgerufen werden, kann
durch Abrundung dieser Ecken eine Erhöhung der Durchbruchspannung in
diesen Bereichen erzielt werden.
-Übergänge bedingen kleine
Radien und
verringern die Durchbruchspannung. Für Leistungsbauelemente sind daher oft
zusätzliche Prozeßschritte (Diffusionen) notwendig, um tiefere Übergänge
zu erzielen. Da sphärische Übergänge durch Aufeinandertreffen von
zylindrischen Übergängen an Ecken der Struktur hervorgerufen werden, kann
durch Abrundung dieser Ecken eine Erhöhung der Durchbruchspannung in
diesen Bereichen erzielt werden.
Positive Oberflächenladungen über dem Verarmungsgebiet einer in einem
 -Gebiet liegenden
-Gebiet liegenden 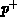 -Schicht verstärken die Krümmung der
Raumladungszone und verringern die Durchbruchspannung, negative Ladungen
verringern die Krümmung und erhöhen damit die Durchbruchspannung. Für
eine in einem
-Schicht verstärken die Krümmung der
Raumladungszone und verringern die Durchbruchspannung, negative Ladungen
verringern die Krümmung und erhöhen damit die Durchbruchspannung. Für
eine in einem 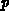 -Gebiet liegende
-Gebiet liegende 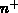 -Schicht gilt obiges mit vertauschten
Vorzeichen.
-Schicht gilt obiges mit vertauschten
Vorzeichen.
Es sind einige Techniken entwickelt worden, um durch eine Verringerung des
Krümmungsradius die Durchbruchspannung zu erhöhen. Diese sollen nur kurz
aufgeführt werden, da sie für die hier behandelte Technologie nicht
explizit verwendet werden (allerdings haben sie zum Teil eine implizite
Bedeutung, siehe z.B. Abschnitt 3.1.2).
- Feldringe:
- In einiger Distanz vom
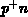 -Übergang werden im niedrig
dotierten
-Übergang werden im niedrig
dotierten  -Gebiet nicht kontaktierte (floating) Ringe mit hoher
-Gebiet nicht kontaktierte (floating) Ringe mit hoher
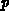 -Dotierung eingebracht. Reicht die Raumladungszone bis zu
den Feldringen, nehmen sie das Potential der Raumladungszone an dieser Stelle
an. Es bildet sich von ihnen ausgehend ebenfalls eine Raumladungszone im
niedrig dotierten Gebiet, die jedoch aufgrund der geringeren
Potentialdifferenz zur Spannung des
-Dotierung eingebracht. Reicht die Raumladungszone bis zu
den Feldringen, nehmen sie das Potential der Raumladungszone an dieser Stelle
an. Es bildet sich von ihnen ausgehend ebenfalls eine Raumladungszone im
niedrig dotierten Gebiet, die jedoch aufgrund der geringeren
Potentialdifferenz zur Spannung des  -Gebiets außerhalb der
Raumladungszone (die restliche
Spannung fällt ja bis zu den Feldringen vom
-Gebiets außerhalb der
Raumladungszone (die restliche
Spannung fällt ja bis zu den Feldringen vom 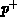 -Gebiet her ab) schmäler
ist als die vom eigentlichen
-Gebiet her ab) schmäler
ist als die vom eigentlichen  -Übergang herrührende. Da die Weite der
Raumladungszone wesentlich die Durchbruchspannung beeinflußt, wird dadurch
die Durchbruchspannung erhöht. Es sind viele Variationen dieses Konzepts
möglich, so z.B. auch mehrfache Feldringe [135].
-Übergang herrührende. Da die Weite der
Raumladungszone wesentlich die Durchbruchspannung beeinflußt, wird dadurch
die Durchbruchspannung erhöht. Es sind viele Variationen dieses Konzepts
möglich, so z.B. auch mehrfache Feldringe [135].
- Feldplatten:
- Werden an einem
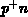 -Übergang über dem
-Übergang über dem  -Gebiet eine
isolierende Schicht und darüber ein Kontakt angebracht, so kann man damit
den Verlauf der sich darunter ausbildenden Raumladungszone beeinflussen.
Macht man die Spannung an der Feldplatte negativer, so
verringert man die Krümmung der Raumladungszone (sofern diese im Bereich
der Feldplatte liegt), erhöht man die Spannung, dann verstärkt man die
Krümmung. Für
-Gebiet eine
isolierende Schicht und darüber ein Kontakt angebracht, so kann man damit
den Verlauf der sich darunter ausbildenden Raumladungszone beeinflussen.
Macht man die Spannung an der Feldplatte negativer, so
verringert man die Krümmung der Raumladungszone (sofern diese im Bereich
der Feldplatte liegt), erhöht man die Spannung, dann verstärkt man die
Krümmung. Für 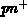 -Übergänge gilt obiges vice versa. Die Dicke des
Oxids ist ein wesentlicher Parameter. Für sehr hohe Spannungen werden auch
multistep-Feldplatten verwendet [35].
-Übergänge gilt obiges vice versa. Die Dicke des
Oxids ist ein wesentlicher Parameter. Für sehr hohe Spannungen werden auch
multistep-Feldplatten verwendet [35].
Die Fortsetzung des Kontakts der hoch dotierten Schicht auf einer
Oxidschicht über den 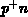 -Übergang in das niedrig dotierte Gebiet hat
ähnliche Wirkung, da (bei gesperrtem
-Übergang in das niedrig dotierte Gebiet hat
ähnliche Wirkung, da (bei gesperrtem 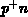 -Übergang) das Potential der
Feldplatte niedriger ist als das der Raumladungszone im
-Übergang) das Potential der
Feldplatte niedriger ist als das der Raumladungszone im  -Gebiet.
-Gebiet.
- Schräge Bauteilkanten:
- Durch einfaches Ab- oder Einschneiden (oder
-ätzen) des Wafers senkrecht zur Oberfläche oder in einem positiven
oder negativen Winkel dazu im Bereich eines gekrümmten
 -Übergangs
können Feldstärkespitzen verhindert oder
verringert werden. Diese Technik ist aber lediglich für diskrete
Bauelemente und keinesfalls für integrierte Schaltungen möglich.
-Übergangs
können Feldstärkespitzen verhindert oder
verringert werden. Diese Technik ist aber lediglich für diskrete
Bauelemente und keinesfalls für integrierte Schaltungen möglich.
In [41] wird ein Vergleich der Wirkung von Feldringen und
Feldplatten mit Hilfe von numerischen Simulationen durchgeführt. Es zeigt
sich, daß sich für optimale Designs beider Methoden (es wird ein einfacher
Feldring verwendet) für Tiefen des  -Übergangs von
-Übergangs von 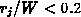 mit
der Feldplatte eine höhere Durchbruchspannung erzielen läßt, für tiefere
Übergänge mit Feldringen.
mit
der Feldplatte eine höhere Durchbruchspannung erzielen läßt, für tiefere
Übergänge mit Feldringen.
In lateralen Bauelementen wie dem LDMOS-Transistor kann die
Oberflächenfeldstärke dadurch reduziert werden, daß man das Driftgebiet
als dünne, verhältnismäßig hochohmige epitaktische Schicht
ausführt (REduced SURface Field,
RESURF) [5][33][45][58].
Die niedrige Dotierung dieser Epi-Schicht bringt allerdings einen hohen
On-Widerstand mit sich. Gegenmaßnahmen können eine multiple resistivity-Driftregion [78], Implantationen in das
Driftgebiet und die Verwendung von Widerstandsmaterial, das auf dem Oxid
über der Driftzone angebracht wird (etwa aus polykristallinem Silizium
SIPOS) [21][58], enthalten.
Auch die Verwendung von
internen Feldringen bei LDMOS-Transistoren (Feldringe innerhalb der
Driftstrecke) wurde vorgeschlagen [86]. Mit diesen Mitteln können
LDMOS-Transistoren mit hohen Vorwärts-Blockierspannungen realisiert
werden [74]. Einen Überblick über laterale MOS-Gate-gesteuerte
Leistungsbauelemente gibt [28].




Next: 2.1.2 Die Kontaktierung des
Up: 2.1 DMOS-Grundstrukturen
Previous: 2.1 DMOS-Grundstrukturen
Martin Stiftinger
Wed Oct 5 11:53:06 MET 1994
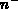 -Substrat dient als sog. Driftzone, die hohe
Drainspannungen aufnehmen kann. Mit dieser Dotierung ist ein
verhältnismäßig hoher Widerstand verbunden, der bei Stromfluß einen
Großteil der Drain-Source-Spannung aufnimmt, sodaß am Kanal selbst nur ein
Bruchteil dieser Spannung abfällt.
-Substrat dient als sog. Driftzone, die hohe
Drainspannungen aufnehmen kann. Mit dieser Dotierung ist ein
verhältnismäßig hoher Widerstand verbunden, der bei Stromfluß einen
Großteil der Drain-Source-Spannung aufnimmt, sodaß am Kanal selbst nur ein
Bruchteil dieser Spannung abfällt.




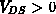 ) der
) der  -Übergang zwischen
-Übergang zwischen
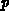 -body und Driftgebiet gesperrt. Es bildet sich eine
Raumladungszone, die die Drain-Source-Spannung aufnehmen muß. Eine
Raumladungszone um einen
-body und Driftgebiet gesperrt. Es bildet sich eine
Raumladungszone, die die Drain-Source-Spannung aufnehmen muß. Eine
Raumladungszone um einen 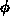 , dem elektrischen Feld
, dem elektrischen Feld 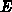 in
in
 -Richtung, der Raumladung
-Richtung, der Raumladung 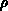 zufolge der ionisierten
Akzeptor- und Donatorkonzentrationen
zufolge der ionisierten
Akzeptor- und Donatorkonzentrationen 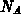 und
und 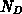 in der Raumladungszone)
lautet:
in der Raumladungszone)
lautet:
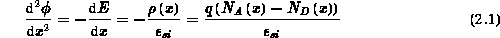
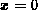 mit
mit
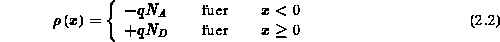
 -Gebiet:
-Gebiet:
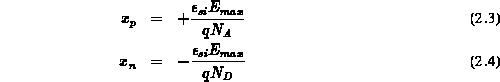
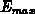 ist negativ und folgt mit der in Sperrichtung angelegten
Spannung
ist negativ und folgt mit der in Sperrichtung angelegten
Spannung  zu:
zu:
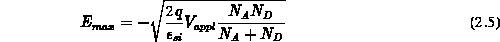
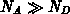 oder
umgekehrt). Je niedriger dieses dotiert ist, desto geringer ist die maximale
Feldstärke (sie tritt immer im metallurgischen
oder
umgekehrt). Je niedriger dieses dotiert ist, desto geringer ist die maximale
Feldstärke (sie tritt immer im metallurgischen 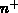 -Sourcegebiet erreicht, da es sonst zum sog. punch
through-Durchbruch kommt.
-Sourcegebiet erreicht, da es sonst zum sog. punch
through-Durchbruch kommt.
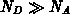 wird in
wird in
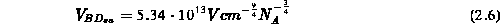
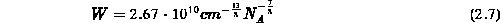


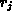 ist der Radius des
ist der Radius des 
 entstehen. Für einen
abrupten, sphärischen Übergang kann die Poissongleichung in
Kugelkoordinaten gelöst werden. Die Durchbruchspannung ergibt sich im
Vergleich zu der eines ebenen, abrupten Übergangs
zu
entstehen. Für einen
abrupten, sphärischen Übergang kann die Poissongleichung in
Kugelkoordinaten gelöst werden. Die Durchbruchspannung ergibt sich im
Vergleich zu der eines ebenen, abrupten Übergangs
zu 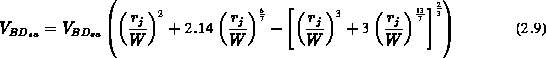
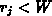 und
für eine Hintergrunddotierung kleiner als
und
für eine Hintergrunddotierung kleiner als 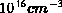 (ein sehr hoher
Wert für die Grunddotierung).
Abb.
(ein sehr hoher
Wert für die Grunddotierung).
Abb. 
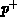 -Schicht verstärken die Krümmung der
Raumladungszone und verringern die Durchbruchspannung, negative Ladungen
verringern die Krümmung und erhöhen damit die Durchbruchspannung. Für
eine in einem
-Schicht verstärken die Krümmung der
Raumladungszone und verringern die Durchbruchspannung, negative Ladungen
verringern die Krümmung und erhöhen damit die Durchbruchspannung. Für
eine in einem 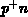 -Übergang werden im niedrig
dotierten
-Übergang werden im niedrig
dotierten 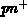 -Übergänge gilt obiges vice versa. Die Dicke des
Oxids ist ein wesentlicher Parameter. Für sehr hohe Spannungen werden auch
multistep-Feldplatten verwendet [35].
-Übergänge gilt obiges vice versa. Die Dicke des
Oxids ist ein wesentlicher Parameter. Für sehr hohe Spannungen werden auch
multistep-Feldplatten verwendet [35].
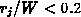 mit
der Feldplatte eine höhere Durchbruchspannung erzielen läßt, für tiefere
Übergänge mit Feldringen.
mit
der Feldplatte eine höhere Durchbruchspannung erzielen läßt, für tiefere
Übergänge mit Feldringen.