5.3 Die Quasisättigung




Next: 5.4 Der Kanal
Up: 5 Numerische Bauelementsimulation von
Previous: 5.2 Die DC-Kennlinien
Da der Stromtransport in MOS-Bauelementen nur von einer Ladungsträgerart
bewerkstelligt wird, genügt es im Fall des  -Kanal DMOS-Transistors, die
Elektronenkonzentration im Bauelement zu betrachten, um die Ausdehnung des
Stromflußgebiets zu untersuchen. In den folgenden drei Abbildungen ist das
Gebiet hoher Elektronenkonzentration und damit das Stromflußgebiet
dargestellt. Dies ist in der Form von Höhenschichtlinien bei einer
Konzentration von
-Kanal DMOS-Transistors, die
Elektronenkonzentration im Bauelement zu betrachten, um die Ausdehnung des
Stromflußgebiets zu untersuchen. In den folgenden drei Abbildungen ist das
Gebiet hoher Elektronenkonzentration und damit das Stromflußgebiet
dargestellt. Dies ist in der Form von Höhenschichtlinien bei einer
Konzentration von 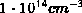 erfolgt. Wie später noch
gezeigt wird, ändert sich die Elektronenkonzentration fast abrupt auf
beinahe verschwindende Größe. Der
genaue Wert, bei dem die Höhenschichtlinie eingezeichnet wird, ist somit
praktisch irrelevant, sofern er sich in einem sinnvollen Bereich zwischen
etwa
erfolgt. Wie später noch
gezeigt wird, ändert sich die Elektronenkonzentration fast abrupt auf
beinahe verschwindende Größe. Der
genaue Wert, bei dem die Höhenschichtlinie eingezeichnet wird, ist somit
praktisch irrelevant, sofern er sich in einem sinnvollen Bereich zwischen
etwa 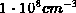 und
und 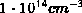 befindet. Gerade
die Kenntnis der Grenzen dieses Bereichs macht es sinnvoller, die
Elektronenkonzentration und nicht die Stromdichte für die Bestimmung der
Stromflußgebiete zu verwenden. Diese sind für den Fall der
Sättigung (
befindet. Gerade
die Kenntnis der Grenzen dieses Bereichs macht es sinnvoller, die
Elektronenkonzentration und nicht die Stromdichte für die Bestimmung der
Stromflußgebiete zu verwenden. Diese sind für den Fall der
Sättigung (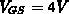 ), für den Übergang zwischen Sättigung
und Quasisättigung (
), für den Übergang zwischen Sättigung
und Quasisättigung (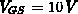 ) und für Quasisättigung (
) und für Quasisättigung (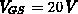 ) bei mehreren Drainspannungen in den Abbildungen Abb. 5.6,
Abb. 5.7 und Abb. 5.10 dargestellt.
) bei mehreren Drainspannungen in den Abbildungen Abb. 5.6,
Abb. 5.7 und Abb. 5.10 dargestellt.
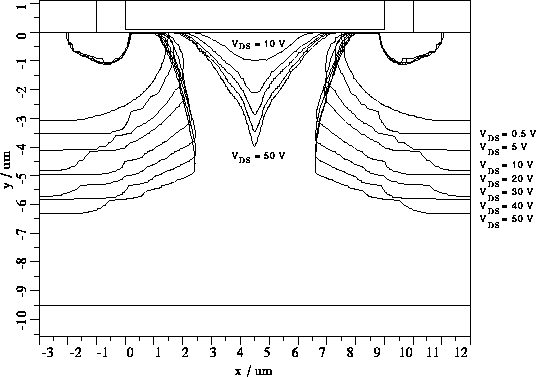
Abbildung 5.6: Stromflußgebiete für 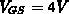 .
.
Im Fall von 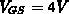 zeigt sich für Drainspannungen kleiner
zeigt sich für Drainspannungen kleiner 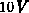 der erwartete JFET-Effekt mit sich lateral und vertikal
ausdehnenden seitlichen Raumladungszonen. Das Stromflußgebiet weitet sich
zum buried layer hin für diese niedrigen Drainspannungen mit einem
Winkel von etwa
der erwartete JFET-Effekt mit sich lateral und vertikal
ausdehnenden seitlichen Raumladungszonen. Das Stromflußgebiet weitet sich
zum buried layer hin für diese niedrigen Drainspannungen mit einem
Winkel von etwa 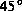 auf.
auf.
Für 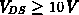 bildet sich allerdings auch eine
Raumladungszone von der Mitte der Grenzfläche Driftgebiet-Gateoxid lateral
und vertikal aus. Das Potential an der Grenzfläche steigt zur Mitte des
Driftgebiets hin an und übersteigt den zur Akkumulation notwendigen Wert
(siehe Abb. 5.23). Mit steigender Drainspannung dehnen sich sowohl die
seitlichen Raumladungszonen als auch die Raumladungszone in der Mitte der
Driftzone lateral und vertikal aus. Der Winkel der Stromaufweitung am
,,unteren`` Ende der seitlichen Raumladungszonen steigt mit zunehmender
Drainspannung.
bildet sich allerdings auch eine
Raumladungszone von der Mitte der Grenzfläche Driftgebiet-Gateoxid lateral
und vertikal aus. Das Potential an der Grenzfläche steigt zur Mitte des
Driftgebiets hin an und übersteigt den zur Akkumulation notwendigen Wert
(siehe Abb. 5.23). Mit steigender Drainspannung dehnen sich sowohl die
seitlichen Raumladungszonen als auch die Raumladungszone in der Mitte der
Driftzone lateral und vertikal aus. Der Winkel der Stromaufweitung am
,,unteren`` Ende der seitlichen Raumladungszonen steigt mit zunehmender
Drainspannung.
Die Einengung des Strompfads durch die Raumladungszone in der Mitte der
Driftzone mit steigender Drainspannung bringt allerdings
keine wesentliche Erhöhung des Gesamtwiderstands mit sich, da der
Drainstrom mit steigender Drainspannung leicht ansteigt. Die in
[131] mit dieser Einschnürung erklärten negativen
Ausgangsleitwerte bei Messungen konnten durch diese Simulationen nicht
verifiziert werden. Sie sind allerdings leicht mit der bei Messungen von
Leistungsbauelementen auftretenden Erwärmung der Bauelemente erklärbar
(siehe Kapitel 6.7.2).

Abbildung 5.7: Stromflußgebiete für 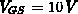 .
.
Für 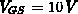 (Übergang Sättigung-Quasisättigung) tritt keine
Raumladungszone an der Grenzfläche Driftzone-Gateoxid auf. Die Differenz
zwischen Gate- und Grenzschichtpotential bleibt immer über der
Akkumulationsbedingung (vergleiche auch Abb. 5.24). Die seitlichen
Raumladungszonen dehnen sich mit steigender Drainspannung lateral und
vertikal aus. Auffällig ist aber, daß die laterale Ausdehnung nur sehr
gering ist, es
also keineswegs zu einer Abschnürung (pinch-off) des Stromflußpfads
durch laterales Zusammenwachsen der Raumladungszone in der Mitte des
Driftgebiets kommt. Die beginnende Quasisättigung kann somit nicht allein
durch den JFET-Effekt erklärt werden, wie dies lange Zeit getan wurde.
(Übergang Sättigung-Quasisättigung) tritt keine
Raumladungszone an der Grenzfläche Driftzone-Gateoxid auf. Die Differenz
zwischen Gate- und Grenzschichtpotential bleibt immer über der
Akkumulationsbedingung (vergleiche auch Abb. 5.24). Die seitlichen
Raumladungszonen dehnen sich mit steigender Drainspannung lateral und
vertikal aus. Auffällig ist aber, daß die laterale Ausdehnung nur sehr
gering ist, es
also keineswegs zu einer Abschnürung (pinch-off) des Stromflußpfads
durch laterales Zusammenwachsen der Raumladungszone in der Mitte des
Driftgebiets kommt. Die beginnende Quasisättigung kann somit nicht allein
durch den JFET-Effekt erklärt werden, wie dies lange Zeit getan wurde.
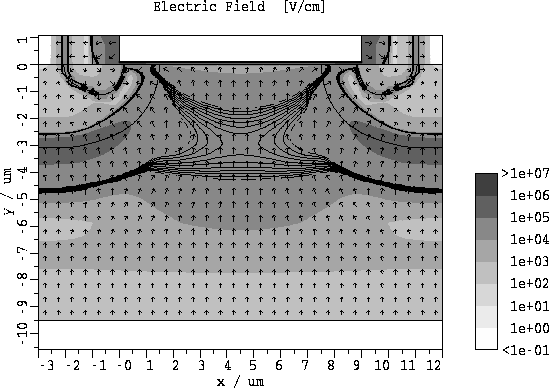
Abbildung 5.8: Elektrisches Feld fuer 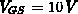 und
und 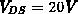 mit Isolinien fuer
mit Isolinien fuer 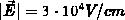 bis
bis 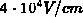 .
.
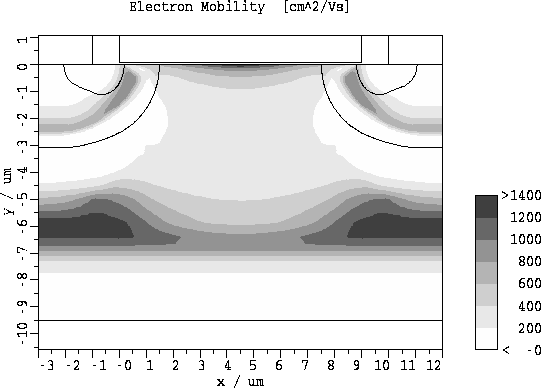
Abbildung 5.9: Elektronenbeweglichkeit fuer
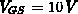 und
und 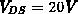 .
.
Abb. 5.8 zeigt das elektrische Feld für 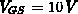 und
und 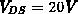 . Im Bereich der
Einschnürung ergibt sich ein elektrisches Feld mit Werten größer
. Im Bereich der
Einschnürung ergibt sich ein elektrisches Feld mit Werten größer 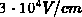 . Dies ist im Bereich der elektrischen Feldstärke, bei der die
Driftgeschwindigkeit sättigt (aus Messungen [20][19] und
Monte-Carlo-Simulationen [66] ergibt sich ein Wert von ca.
. Dies ist im Bereich der elektrischen Feldstärke, bei der die
Driftgeschwindigkeit sättigt (aus Messungen [20][19] und
Monte-Carlo-Simulationen [66] ergibt sich ein Wert von ca. 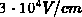 für die kritische Feldstärke). Dies erklärt auch die in
diesem Bereich niedrige Elektronenbeweglichkeit (siehe Abb. 5.9). Man
kann also die Geschwindigkeitssättigung in der Driftzone (genauer im
JFET-Gebiet) als hauptsächliche Ursache für die Stromsättigung
identifizieren [26].
für die kritische Feldstärke). Dies erklärt auch die in
diesem Bereich niedrige Elektronenbeweglichkeit (siehe Abb. 5.9). Man
kann also die Geschwindigkeitssättigung in der Driftzone (genauer im
JFET-Gebiet) als hauptsächliche Ursache für die Stromsättigung
identifizieren [26].
Für den Fall der Quasisättigung (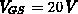 ) tritt oben Gesagtes
noch deutlicher zutage. Das Stromflußgebiet in Abhängigkeit der
Drainspannung bildet sich fast identisch zum Fall für
) tritt oben Gesagtes
noch deutlicher zutage. Das Stromflußgebiet in Abhängigkeit der
Drainspannung bildet sich fast identisch zum Fall für 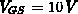 aus.
Allerdings tritt jetzt praktisch überhaupt keine laterale Ausweitung der
Raumladungszonen mit steigender Drainspannung mehr auf (siehe
Abb. 5.10).
aus.
Allerdings tritt jetzt praktisch überhaupt keine laterale Ausweitung der
Raumladungszonen mit steigender Drainspannung mehr auf (siehe
Abb. 5.10).
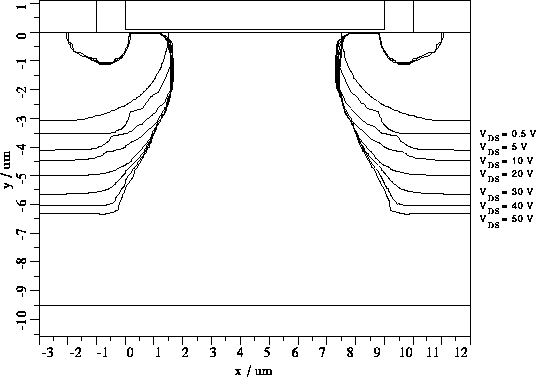
Abbildung 5.10: Stromflußgebiete für  .
.
Die Abbildungen 5.11 und 5.12 zeigen, daß sich die
Gebiete mit hohem elektrischen Feld und niedriger Elektronenbeweglichkeit
weiter ausdehnen.
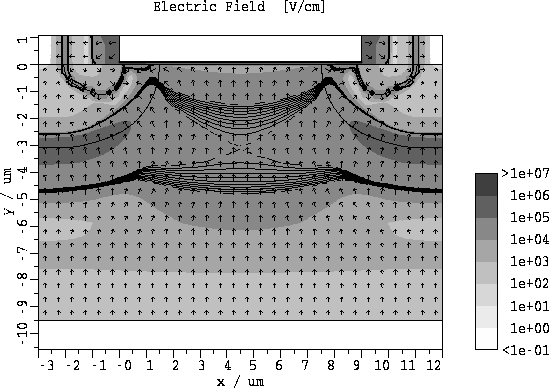
Abbildung 5.11: Elektrisches Feld fuer  und
und 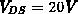 mit Isolinien fuer
mit Isolinien fuer 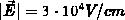 bis
bis 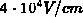 .
.
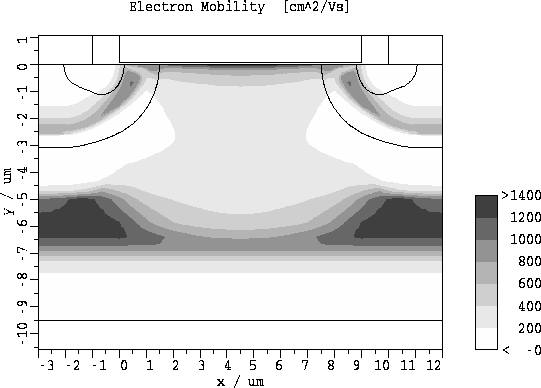
Abbildung 5.12: Elektronenbeweglichkeit fuer
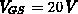 und
und 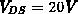 .
.
Elektronenbeweglichkeit für 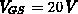 und
und 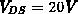 .
.
Interessante Details betreffend die Elektronen- und Potentialverteilung in
der Driftzone sollen im folgenden gezeigt werden. Abb. 5.13 zeigt
einen vertikalen Schnitt in der Symmetrieachse in der Mitte der Driftzone
für 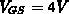 .
Es sind die Verläufe für die Elektronenkonzentration (logarithmisch,
durchgezogene Linien, in
.
Es sind die Verläufe für die Elektronenkonzentration (logarithmisch,
durchgezogene Linien, in 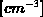 ) und das elektrostatische Potential
(strichlierte Linien, in
) und das elektrostatische Potential
(strichlierte Linien, in 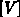 ) dargestellt.
) dargestellt.
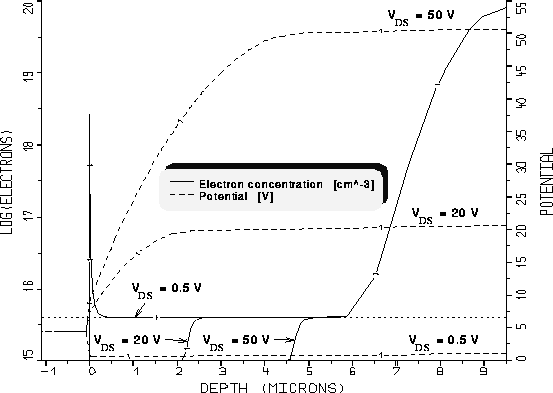
Abbildung 5.13: Elektronen- und Potentialverteilung im
vertikalen Schnitt in der Mitte der Driftzone eines DMOS-Transistors
bei 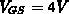 .
.
Für 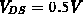 fällt das Potential im Gateoxid auf einen Wert ab,
der etwas unter jenem am Drainkontakt liegt (dabei ist natürlich das
Kontaktpotential berücksichtigt). Im Driftgebiet steigt es also leicht
bis zum Drainkontakt an. Dieses Minimum im vertikalen Potentialverlauf kann
für die höheren eingezeichneten Drainspannungen nicht beobachtet werden.
Im Gegensatz zum Fall für
fällt das Potential im Gateoxid auf einen Wert ab,
der etwas unter jenem am Drainkontakt liegt (dabei ist natürlich das
Kontaktpotential berücksichtigt). Im Driftgebiet steigt es also leicht
bis zum Drainkontakt an. Dieses Minimum im vertikalen Potentialverlauf kann
für die höheren eingezeichneten Drainspannungen nicht beobachtet werden.
Im Gegensatz zum Fall für 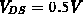 tritt für die höheren
Drainspannungen auch keine Akkumulation von Elektronen an der Grenzfläche
in der Mitte der Driftzone auf. In Übereinstimmung mit Abb. 5.6
steigen die Elektronenkonzentrationen in diesen Fällen von sehr kleinen
Werten bei ca.
tritt für die höheren
Drainspannungen auch keine Akkumulation von Elektronen an der Grenzfläche
in der Mitte der Driftzone auf. In Übereinstimmung mit Abb. 5.6
steigen die Elektronenkonzentrationen in diesen Fällen von sehr kleinen
Werten bei ca. 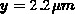 bzw.
bzw. 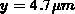 auf die
Dotierungskonzentration in der Driftzone (
auf die
Dotierungskonzentration in der Driftzone (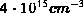 ,
punktierte Linie) an (es ist zu beachten, daß in den 2D-Darstellungen die
vertikale Koordinate negativ in die Tiefe des Transistors gezählt wird, in
den 1D-Schnitten aber positiv). Es fällt die gesamte Spannung der Driftzone
in dieser Schnittebene über der Raumladungszone ab, praktisch keine mehr in
jenem Teil des Driftgebiets, in dem die Elektronenkonzentration angestiegen
ist.
,
punktierte Linie) an (es ist zu beachten, daß in den 2D-Darstellungen die
vertikale Koordinate negativ in die Tiefe des Transistors gezählt wird, in
den 1D-Schnitten aber positiv). Es fällt die gesamte Spannung der Driftzone
in dieser Schnittebene über der Raumladungszone ab, praktisch keine mehr in
jenem Teil des Driftgebiets, in dem die Elektronenkonzentration angestiegen
ist.
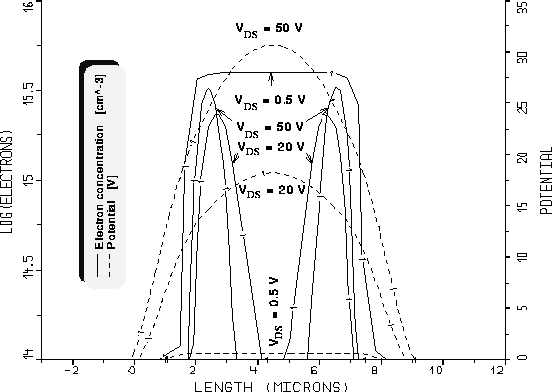
Abbildung 5.14: Elektronen- und Potentialverteilung im
lateralen Schnitt in 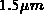 Tiefe bei
Tiefe bei 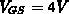 .
.
Abb. 5.14 zeigt einen lateralen Schnitt durch das Driftgebiet in
einer Tiefe von 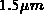 unterhalb der Siliziumoberfläche bei
unterhalb der Siliziumoberfläche bei 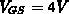 . Es sind die gleichen Größen wie in Abb. 5.13 dargestellt. Für
. Es sind die gleichen Größen wie in Abb. 5.13 dargestellt. Für
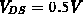 sind sowohl Elektronenkonzentration als auch Potential
lateral über das Stromflußgebiet beinahe konstant. Besonders die
Elektronenkonzentration ist relativ scharf zu den seitlichen
Raumladungszonen begrenzt. Die charakteristische Länge für den Abfall der
Konzentration zu einer Raumladungszone hin ist die Debye-Länge
[116]:
sind sowohl Elektronenkonzentration als auch Potential
lateral über das Stromflußgebiet beinahe konstant. Besonders die
Elektronenkonzentration ist relativ scharf zu den seitlichen
Raumladungszonen begrenzt. Die charakteristische Länge für den Abfall der
Konzentration zu einer Raumladungszone hin ist die Debye-Länge
[116]:
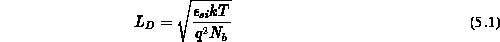
Die Elektronenkonzentrationen für die höheren eingezeichneten
Drainspannungen weisen neben der zusätzlichen Raumladungszone in der Mitte
der Driftzone auch geringere Maximalwerte auf. Die Potentialverteilung ist
über dem Stromflußgebiet in lateraler Richtung nicht konstant und weist in
der Mitte der Driftzone ein ausgeprägtes Maximum auf.
Bei einer Gatespannung von 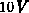 (siehe Abb. 5.15) weisen
Elektronenkonzentration und Potential in vertikaler Richtung (wie oben in
der Mitte der Driftzone) qualitativ gleiche Verläufe auf wie für
(siehe Abb. 5.15) weisen
Elektronenkonzentration und Potential in vertikaler Richtung (wie oben in
der Mitte der Driftzone) qualitativ gleiche Verläufe auf wie für 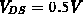 bei
bei 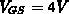 (vgl. Abb. 5.13).
(vgl. Abb. 5.13).
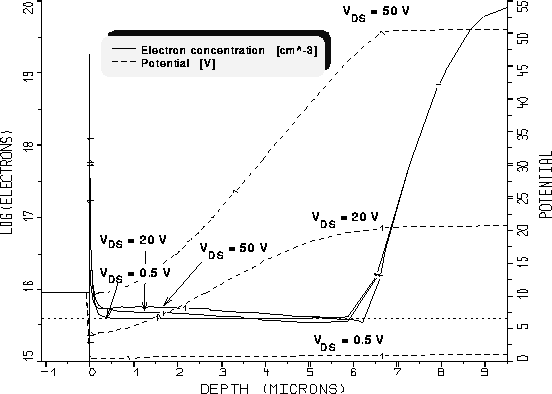
Abbildung 5.15: Elektronen- und Potentialverteilung im
vertikalen Schnitt in der Mitte der Driftzone eines DMOS-Transistors
bei 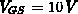 .
.
Jedoch tritt nun auch bei den höheren Drainspannungen Akkumulation der
Elektronen an der Grenzfläche zum Gateoxid auf. Am Rande der
Akkumulationsschicht sinkt die Elektronenkonzentration bei den höheren
Drainspannungen allerdings nicht auf den Wert der Epi-Dotierung ab, sondern
nimmt von einem deutlich darüberliegenden Wert (der wiederum von der
Drainspannung abhängt) zum buried layer hin ab und unterschreitet
die Epi-Dotierung sogar. Besonders bei 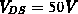 erstreckt sich dieser
Bereich auch in den buried layer.
erstreckt sich dieser
Bereich auch in den buried layer.
Es entsteht somit ein Dipol (ähnliches wird in JFETs beobachtet
[68]): In jenem Bereich, in dem die Elektronenkonzentration die
Epi-Dotierung übersteigt, ergibt sich eine negative Raumladung, in jenem,
wo sie kleiner als die Epi-Dotierung ist, eine positive. In
Abb. 5.16 und Abb. 5.17 ist der Betrag der Raumladungsdichte mit
den Grenzen zwischen positiver und negativer Raumladung dargestellt. Da sich
die positive Raumladung bis in den buried layer ausdehnen kann (deutlich
bei 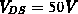 erkennbar), dehnt sich dadurch auch das Gebiet, in dem
die Gate-Drain-Spannung abfällt, bis in diesen hinein aus. Dies ist deutlich
aus Abb. 5.15 erkennbar.
erkennbar), dehnt sich dadurch auch das Gebiet, in dem
die Gate-Drain-Spannung abfällt, bis in diesen hinein aus. Dies ist deutlich
aus Abb. 5.15 erkennbar.
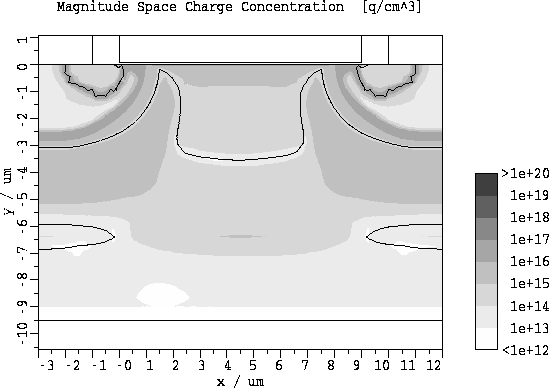
Abbildung 5.16: Betrag der Raumladungsdichte
fuer 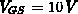 und
und 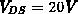 .
.
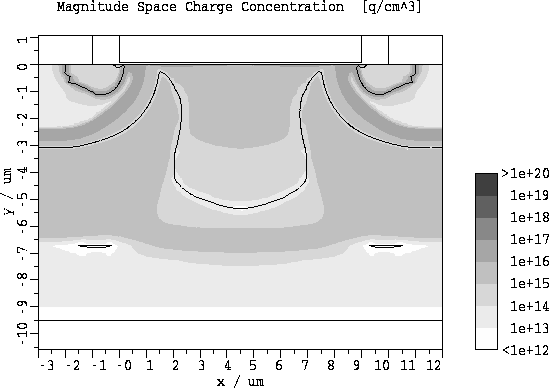
Abbildung 5.17: Betrag der Raumladungsdichte
fuer 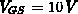 und
und 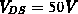 .
.
Aus Abb. 5.18, in der die Elektronen- und Potentialverteilung in einem
lateralen Schnitt an derselben Stelle wie in Abb. 5.14 dargestellt
sind, erkennt man, daß die Elektronenkonzentrationen wie auch die
Potentialverteilungen für diesen Fall (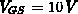 ) im Stromflußgebiet
lateral annähernd konstant sind. Eine Erhöhung der Drainspannung von
) im Stromflußgebiet
lateral annähernd konstant sind. Eine Erhöhung der Drainspannung von 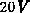 auf
auf 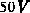 bewirkt eine Verstärkung des Dipol-Effekts (höhere
Elektronenkonzentration im Stromflußgebiet), aber keine weitere
Einschnürung durch die seitlichen Raumladungszonen. Diese Erhöhung der
Elektronenkonzentration im Gebiet des schmalsten Stromflußquerschnitts im
Driftgebiet ist für das Ansteigen des Drainstroms mit steigender
Drainspannung verantwortlich (siehe Abb. 5.4). Zur Aufrechterhaltung
der Ladungsneutralität ist die Ausbildung einer positiven Raumladung im
an den buried layer angrenzenden Gebiet notwendig.
bewirkt eine Verstärkung des Dipol-Effekts (höhere
Elektronenkonzentration im Stromflußgebiet), aber keine weitere
Einschnürung durch die seitlichen Raumladungszonen. Diese Erhöhung der
Elektronenkonzentration im Gebiet des schmalsten Stromflußquerschnitts im
Driftgebiet ist für das Ansteigen des Drainstroms mit steigender
Drainspannung verantwortlich (siehe Abb. 5.4). Zur Aufrechterhaltung
der Ladungsneutralität ist die Ausbildung einer positiven Raumladung im
an den buried layer angrenzenden Gebiet notwendig.
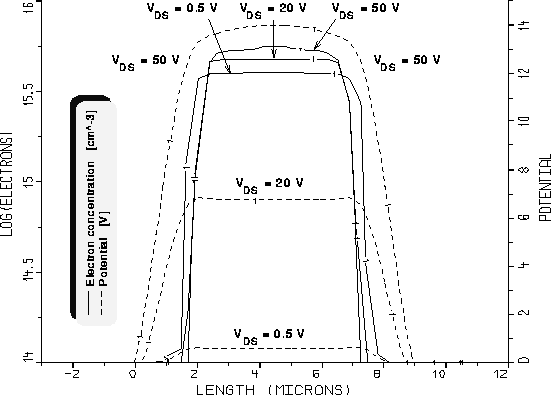
Abbildung 5.18: Elektronen- und Potentialverteilung im
lateralen Schnitt in 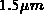 Tiefe bei
Tiefe bei 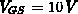 .
.
Die Abbildungen 5.19 und 5.22 zeigen den vertikalen und
lateralen Schnitt für 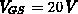 .
Bezüglich des vertikalen
Schnitts (Abb. 5.19) ist im Vergleich zum Fall
.
Bezüglich des vertikalen
Schnitts (Abb. 5.19) ist im Vergleich zum Fall 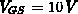 (Abb. 5.15) erwähnenswert, daß das Potential an der
Driftzonenoberfläche für höhere Drainspannungen wesentlich geringer ist.
Dies ist auf eine stärkere Akkumulation zurückzuführen, die einen
geringeren lateralen Akkumulationswiderstand mit sich bringt.
(Abb. 5.15) erwähnenswert, daß das Potential an der
Driftzonenoberfläche für höhere Drainspannungen wesentlich geringer ist.
Dies ist auf eine stärkere Akkumulation zurückzuführen, die einen
geringeren lateralen Akkumulationswiderstand mit sich bringt.
Abbildung 5.19: Elektronen- und Potentialverteilung im
vertikalen Schnitt in der Mitte der Driftzone eines DMOS-Transistors
bei 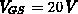 .
.
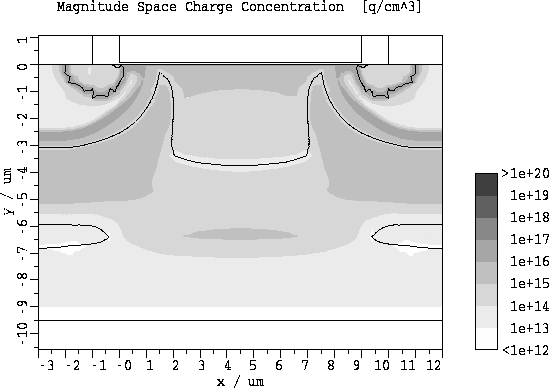
Abbildung 5.20: Betrag der Raumladungsdichte
fuer 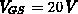 und
und 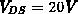 .
.
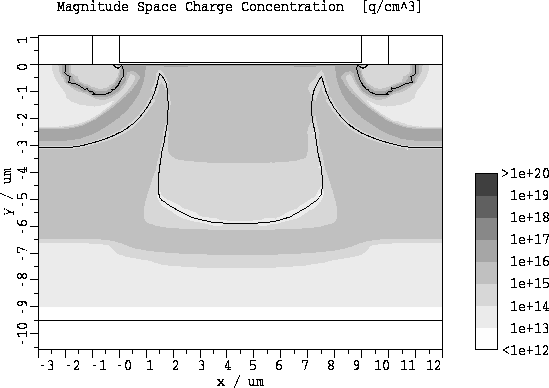
Abbildung 5.21: Betrag der Raumladungsdichte
fuer 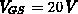 und
und 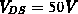 .
.
Ein Vergleich von Abb. 5.20 und Abb. 5.16 bzw. Abb. 5.21
und Abb. 5.17 zeigt, daß sich bei einer Erhöhung der Gatespannung
das Gebiet der negativen Raumladung in der Driftzone (jener Bereich, wo die
Elektronenkonzentration größer als die Epi-Dotierung ist) in lateraler und
vertikaler Richtung ausdehnt.
Im lateralen Verlauf des Potentials (siehe Abb. 5.22) ist
bemerkenswert, daß die negative Raumladung ein Minimum in der Mitte der
Driftzone bewirkt. Dieses ist umso ausgeprägter, je größer die Raumladung
in diesem Gebiet ist.
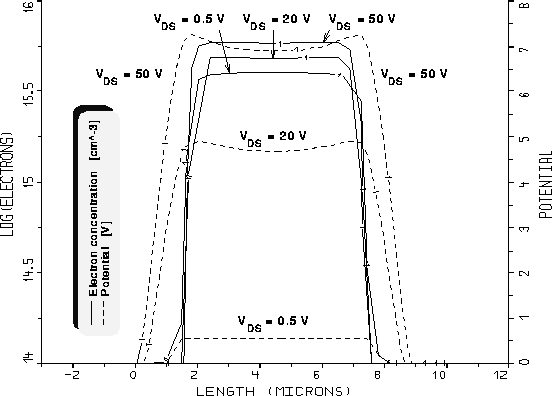
Abbildung 5.22: Elektronen- und Potentialverteilung im
lateralen Schnitt in 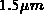 Tiefe bei
Tiefe bei 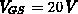 .
.




Next: 5.4 Der Kanal
Up: 5 Numerische Bauelementsimulation von
Previous: 5.2 Die DC-Kennlinien
Martin Stiftinger
Wed Oct 5 11:53:06 MET 1994
 -Kanal DMOS-Transistors, die
Elektronenkonzentration im Bauelement zu betrachten, um die Ausdehnung des
Stromflußgebiets zu untersuchen. In den folgenden drei Abbildungen ist das
Gebiet hoher Elektronenkonzentration und damit das Stromflußgebiet
dargestellt. Dies ist in der Form von Höhenschichtlinien bei einer
Konzentration von
-Kanal DMOS-Transistors, die
Elektronenkonzentration im Bauelement zu betrachten, um die Ausdehnung des
Stromflußgebiets zu untersuchen. In den folgenden drei Abbildungen ist das
Gebiet hoher Elektronenkonzentration und damit das Stromflußgebiet
dargestellt. Dies ist in der Form von Höhenschichtlinien bei einer
Konzentration von 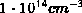 erfolgt. Wie später noch
gezeigt wird, ändert sich die Elektronenkonzentration fast abrupt auf
beinahe verschwindende Größe. Der
genaue Wert, bei dem die Höhenschichtlinie eingezeichnet wird, ist somit
praktisch irrelevant, sofern er sich in einem sinnvollen Bereich zwischen
etwa
erfolgt. Wie später noch
gezeigt wird, ändert sich die Elektronenkonzentration fast abrupt auf
beinahe verschwindende Größe. Der
genaue Wert, bei dem die Höhenschichtlinie eingezeichnet wird, ist somit
praktisch irrelevant, sofern er sich in einem sinnvollen Bereich zwischen
etwa 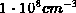 und
und 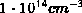 befindet. Gerade
die Kenntnis der Grenzen dieses Bereichs macht es sinnvoller, die
Elektronenkonzentration und nicht die Stromdichte für die Bestimmung der
Stromflußgebiete zu verwenden. Diese sind für den Fall der
Sättigung (
befindet. Gerade
die Kenntnis der Grenzen dieses Bereichs macht es sinnvoller, die
Elektronenkonzentration und nicht die Stromdichte für die Bestimmung der
Stromflußgebiete zu verwenden. Diese sind für den Fall der
Sättigung (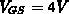 ), für den Übergang zwischen Sättigung
und Quasisättigung (
), für den Übergang zwischen Sättigung
und Quasisättigung (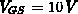 ) und für Quasisättigung (
) und für Quasisättigung (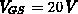 ) bei mehreren Drainspannungen in den Abbildungen Abb. 5.6,
Abb. 5.7 und Abb. 5.10 dargestellt.
) bei mehreren Drainspannungen in den Abbildungen Abb. 5.6,
Abb. 5.7 und Abb. 5.10 dargestellt.





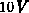 der erwartete JFET-Effekt mit sich lateral und vertikal
ausdehnenden seitlichen Raumladungszonen. Das Stromflußgebiet weitet sich
zum buried layer hin für diese niedrigen Drainspannungen mit einem
Winkel von etwa
der erwartete JFET-Effekt mit sich lateral und vertikal
ausdehnenden seitlichen Raumladungszonen. Das Stromflußgebiet weitet sich
zum buried layer hin für diese niedrigen Drainspannungen mit einem
Winkel von etwa 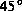 auf.
auf.
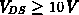 bildet sich allerdings auch eine
Raumladungszone von der Mitte der Grenzfläche Driftgebiet-Gateoxid lateral
und vertikal aus. Das Potential an der Grenzfläche steigt zur Mitte des
Driftgebiets hin an und übersteigt den zur Akkumulation notwendigen Wert
(siehe Abb.
bildet sich allerdings auch eine
Raumladungszone von der Mitte der Grenzfläche Driftgebiet-Gateoxid lateral
und vertikal aus. Das Potential an der Grenzfläche steigt zur Mitte des
Driftgebiets hin an und übersteigt den zur Akkumulation notwendigen Wert
(siehe Abb. 

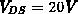 mit Isolinien fuer
mit Isolinien fuer 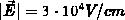 bis
bis 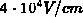 .
.
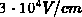 . Dies ist im Bereich der elektrischen Feldstärke, bei der die
Driftgeschwindigkeit sättigt (aus Messungen
. Dies ist im Bereich der elektrischen Feldstärke, bei der die
Driftgeschwindigkeit sättigt (aus Messungen 


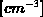 ) und das elektrostatische Potential
(strichlierte Linien, in
) und das elektrostatische Potential
(strichlierte Linien, in 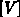 ) dargestellt.
) dargestellt.

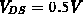 fällt das Potential im Gateoxid auf einen Wert ab,
der etwas unter jenem am Drainkontakt liegt (dabei ist natürlich das
Kontaktpotential berücksichtigt). Im Driftgebiet steigt es also leicht
bis zum Drainkontakt an. Dieses Minimum im vertikalen Potentialverlauf kann
für die höheren eingezeichneten Drainspannungen nicht beobachtet werden.
Im Gegensatz zum Fall für
fällt das Potential im Gateoxid auf einen Wert ab,
der etwas unter jenem am Drainkontakt liegt (dabei ist natürlich das
Kontaktpotential berücksichtigt). Im Driftgebiet steigt es also leicht
bis zum Drainkontakt an. Dieses Minimum im vertikalen Potentialverlauf kann
für die höheren eingezeichneten Drainspannungen nicht beobachtet werden.
Im Gegensatz zum Fall für 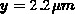 bzw.
bzw. 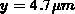 auf die
Dotierungskonzentration in der Driftzone (
auf die
Dotierungskonzentration in der Driftzone (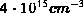 ,
punktierte Linie) an (es ist zu beachten, daß in den 2D-Darstellungen die
vertikale Koordinate negativ in die Tiefe des Transistors gezählt wird, in
den 1D-Schnitten aber positiv). Es fällt die gesamte Spannung der Driftzone
in dieser Schnittebene über der Raumladungszone ab, praktisch keine mehr in
jenem Teil des Driftgebiets, in dem die Elektronenkonzentration angestiegen
ist.
,
punktierte Linie) an (es ist zu beachten, daß in den 2D-Darstellungen die
vertikale Koordinate negativ in die Tiefe des Transistors gezählt wird, in
den 1D-Schnitten aber positiv). Es fällt die gesamte Spannung der Driftzone
in dieser Schnittebene über der Raumladungszone ab, praktisch keine mehr in
jenem Teil des Driftgebiets, in dem die Elektronenkonzentration angestiegen
ist.

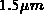 Tiefe bei
Tiefe bei 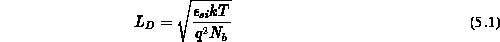

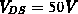 erstreckt sich dieser
Bereich auch in den buried layer.
erstreckt sich dieser
Bereich auch in den buried layer.


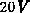 auf
auf 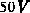 bewirkt eine Verstärkung des Dipol-Effekts (höhere
Elektronenkonzentration im Stromflußgebiet), aber keine weitere
Einschnürung durch die seitlichen Raumladungszonen. Diese Erhöhung der
Elektronenkonzentration im Gebiet des schmalsten Stromflußquerschnitts im
Driftgebiet ist für das Ansteigen des Drainstroms mit steigender
Drainspannung verantwortlich (siehe Abb.
bewirkt eine Verstärkung des Dipol-Effekts (höhere
Elektronenkonzentration im Stromflußgebiet), aber keine weitere
Einschnürung durch die seitlichen Raumladungszonen. Diese Erhöhung der
Elektronenkonzentration im Gebiet des schmalsten Stromflußquerschnitts im
Driftgebiet ist für das Ansteigen des Drainstroms mit steigender
Drainspannung verantwortlich (siehe Abb. 



