 -Netzwerk daraus die Erwärmung
gewonnen. Diese Temperatur wird auch in allen übrigen Modellen des
DMOS-subcircuits übernommen:
-Netzwerk daraus die Erwärmung
gewonnen. Diese Temperatur wird auch in allen übrigen Modellen des
DMOS-subcircuits übernommen:




Im DMOS-Transistor fällt die ohmsche Verlustleistung hauptsächlich im JFET-Bereich an, da dort ein wesentlicher Teil der Spannung abfällt. Diese Leistung wird meist zu einem an der Rückseite des ICs angebrachten Kühlkörper abgeführt.
In einem sehr einfachen Modell wird die im JFET-Bereich umgesetzte Leistung
berechnet und über ein thermisches  -Netzwerk daraus die Erwärmung
gewonnen. Diese Temperatur wird auch in allen übrigen Modellen des
DMOS-subcircuits übernommen:
-Netzwerk daraus die Erwärmung
gewonnen. Diese Temperatur wird auch in allen übrigen Modellen des
DMOS-subcircuits übernommen:
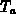 ist die als konstant angenommene Temperatur des Kühlkörpers.
Tatsächlich müssen natürlich die thermischen Widerstände und die
thermischen Kapazitäten mehrerer Schichten (der Kühlkörper liegt nicht
direkt auf dem Silizium auf, für eine genauere Beschreibung siehe etwa
[3]) berücksichtigt werden. Hier soll nur anhand des Siliziums das
Prinzip aufgezeigt werden.
ist die als konstant angenommene Temperatur des Kühlkörpers.
Tatsächlich müssen natürlich die thermischen Widerstände und die
thermischen Kapazitäten mehrerer Schichten (der Kühlkörper liegt nicht
direkt auf dem Silizium auf, für eine genauere Beschreibung siehe etwa
[3]) berücksichtigt werden. Hier soll nur anhand des Siliziums das
Prinzip aufgezeigt werden.
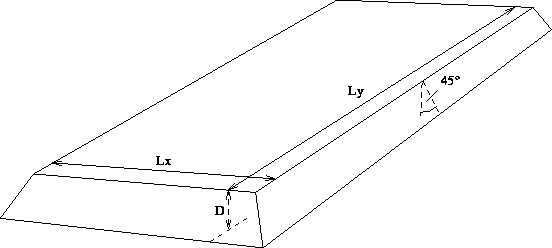
Abbildung 6.16: Wärmeausbreitung in einem DMOS-Block.
Zur Berechnung des thermischen Widerstands und der thermischen Kapazität werden folgende Annahmen getroffen:
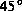 aus.
aus.
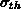 (diese wird als konstant angenommen) geschrieben werden als:
(diese wird als konstant angenommen) geschrieben werden als:
Es ergibt sich für die Geometrie aus Abb. 6.16 folgender thermischer
Widerstand (für insgesamt 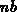 Blöcke und mit
Blöcke und mit 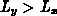 ):
):
Die thermische Kapazität des Siliziums des DMOS-Transistors kann als
Integral des Produkts aus Dichte 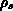 und spezifischer Wärme
und spezifischer Wärme 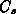 (dieses wird als konstant angenommen) über das Volumen des
Wärmeausdehnungsgebiets berechnet werden:
(dieses wird als konstant angenommen) über das Volumen des
Wärmeausdehnungsgebiets berechnet werden:
Das Ergebnis ergibt sich trivial zu:
Gleichung 6.145 wird in SABER wieder durch automatische Einführung eines virtuellen Knotens, dem die Temperatur des DMOS-Transistors als Variable entspricht, im iterativen Lösungsprozeß mitberücksichtigt (vgl. Abschnitt 6.5.2). Die Gleichungen 6.147 und 6.149 berücksichtigen die Skalierbarkeit des DMOS-Modells.
Um die Temperaturabhängigkeiten des DMOS-Transistors richtig beschreiben zu
können, ist eine zusätzliche Temperaturabhängigkeit des Modells des
Drainwiderstands notwendig. Dies wird durch eine temperaturabhängige
Beweglichkeit für dieses Modell erreicht und durch die einfache
Beziehung 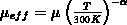 modelliert [105]. Da für den spezifischen elektrischen Widerstand
modelliert [105]. Da für den spezifischen elektrischen Widerstand
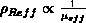 gilt, ist in
Gleichung 6.123 und Gleichung 6.125
gilt, ist in
Gleichung 6.123 und Gleichung 6.125 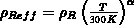 zu setzen. Eine genauere Untersuchung
der thermischen Effekte in der Quasisättigung ist in [70] zu
finden.
zu setzen. Eine genauere Untersuchung
der thermischen Effekte in der Quasisättigung ist in [70] zu
finden.



