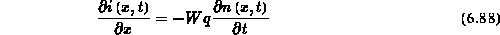
Ausgangspunkt ist die Stromkontinuitätsbeziehung angewendet auf die Inversionsschicht:
Integriert man diese Gleichung nach 
vom sourceseitigen Kanalende
(
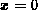) zur Stelle im Kanal, so erhält man:
Nochmalige Integration entlang des gesamten Kanals ergibt mit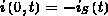 
:
Bei partieller Integration des letzten Terms ergibt sich mit
:
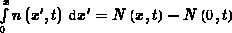Gleichung 6.91 beschreibt eine lineare Gewichtung der beweglichen Ladung entlang des Kanals für ihre Aufteilung in Source- und Drainladung. Gleichung 6.90 lautet dann
mit
und der Sourceladung
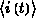stellt den
durchschnittlichen Transportstrom im Kanal dar (in quasistatischer
Betrachtung den DC-Strom). Analog erhält man für den transienten
Drainstrom
und für die Drainladung
Zur Berechnung der Ladungen des MOSFETs nimmt man die Gleichungen für den Drainstrom zu Hilfe.
In der starken Inversion lautet diese (vgl. Gleichung 6.22):
Da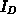 
keine Funktion von ist, kann man daraus
errechnen. So ergibt sich z.B. für die Drainladung:
Setzt man nach Gleichung 6.50 und Gleichung 6.51 für die
Kanalladungsdichte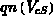 
ein, so erhält man:
Analog erhält man die Sourceladung. Die Bulkladung ergibt sich durch
Integration der Bulkladungsdichte (Gleichung 6.51) von 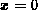bis
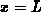zu:
Die Gateladung ergänzt die übrigen Ladungen zu Null.
