Next: 4.2 Lattice and Thermal Up: 4.1 Semiconductor Equations Previous: 4.1.7 Insulator Equations Contents
For the solution of the semiconductor equations a closed domain is required. Boundary conditions for the unknowns in a certain segment must be specified at the boundaries of that segment. Depending on the number of segments (one or two) and the type of the quantity of the unknown (distributed or non-distributed) several model types can be separated [267]. However, in order to illustrate the basic boundary conditions such a differentiation is not needed and therefore not provided here.
The simulation domain usually includes only a single device. In order to separate it from the neighboring devices artificial boundaries, which have no physical origin, are introduced. Through the Neumann boundary conditions a self-contained domain is guaranteed. The fluxes across the boundary are set to zero:
Ohmic contacts are defined by Dirichlet boundary conditions: the
contact potential
![]() , the carrier contact concentration
, the carrier contact concentration
![]() and
and
![]() , and in the case of a HD simulation the
carrier contact temperatures
, and in the case of a HD simulation the
carrier contact temperatures
![]() and
and
![]() are fixed. The metal
quasi-Fermi level (which is specified by the contact potential
are fixed. The metal
quasi-Fermi level (which is specified by the contact potential
![]() ) is equal to the semiconductor quasi-Fermi level. The
model assumes charge-neutrality on the boundary. The contact potential
at the semiconductor boundary is:
) is equal to the semiconductor quasi-Fermi level. The
model assumes charge-neutrality on the boundary. The contact potential
at the semiconductor boundary is:
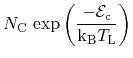 |
(4.32) | ||
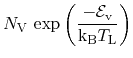 |
(4.33) |
The carrier concentrations in the semiconductor are pinned to the
equilibrium carrier concentrations at the contact:
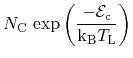 |
(4.34) | ||
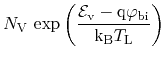 |
(4.35) |
The carrier temperatures
![]() and
and
![]() are set equal to the lattice
temperature
are set equal to the lattice
temperature
![]() :
:
If a contact temperature
![]() is specified, the lattice temperature is
calculated using
is specified, the lattice temperature is
calculated using
![]() and a thermal resistance
and a thermal resistance
![]() . The thermal
heat flow density
. The thermal
heat flow density
![]() at the contact boundary reads:
at the contact boundary reads:
It is possible to include an electric line resistance of the contact
![]() using:
using:
| (4.40) |
At the Schottky contact mixed boundary conditions apply. The
contact potential
![]() , the carrier contact concentration
, the carrier contact concentration
![]() and
and
![]() , and in the case of a HD simulation, the
contact carrier temperatures
, and in the case of a HD simulation, the
contact carrier temperatures
![]() and
and
![]() are fixed. The
semiconductor contact potential is the difference between the metal
quasi-Fermi level and the metal work function difference
are fixed. The
semiconductor contact potential is the difference between the metal
quasi-Fermi level and the metal work function difference
![]() :
:
| (4.43) | |||
| (4.44) |
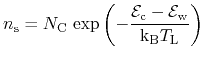 |
(4.45) | ||
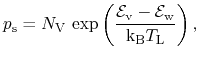 |
(4.46) |
For the equilibrium situation, the quasi-equilibrium concentrations ![]() and
and ![]() can be rewritten:
can be rewritten:
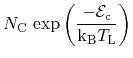 |
(4.47) | ||
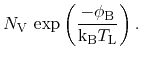 |
(4.48) |
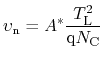 |
(4.49) |
Typical values for the Schottky barrier heights of common semiconductor barriers are listed in Table 4.1. Values measured by different methods (I-V and C-V) for n-GaN/metal differ significantly. This is caused by defects in the surface region, which enhance the tunneling effect and therefore have an impact on the Richardson constant [269,270]. The exact value of the barrier height depends also on orientation, stress, and polarity of the GaN layer [271]. No data is provided for contacts on InN as most metals show ohmic behavior [272]. Schottky barrier height varies with annealing temperature: generally it is reduced after annealing.
| Materials |
|
Ref. | Materials |
|
Ref. |
| n-GaN/Au | 0.87-1.1 | [273,274] | In |
1.56 | [275] |
| n-GaN/Ni | 0.95-1.13 | [273] | In
|
0.75 | [276] |
| p-GaN/Ni | 2.68-2.87 | [277] | p-In
|
0.39 | [278] |
| Al
|
0.94-1.24 | [279] | In
|
0.62 | [270] |
| Al
|
1.26 | [280] | In
|
1.39 | [270] |
| Al
|
1.02-1.30 | [279] | Al
|
0.98-0.93 | [281] |
A model similar to the Schottky contact model is used to calculate the insulator contact potential. The semiconductor contact potential is the difference of the metal quasi-Fermi level and the metal work function difference potential similar to (4.41) and (4.42). The lattice temperature is set equal to the contact temperature (4.38).
In the absence of surface charges the normal component of the dielectric displacement and the potential are continuous:
| (4.50) |
| (4.51) |
At the semiconductor/insulator interface the current densities and heat fluxes normal to the interface vanish.
| (4.52) |
The calculation of the electrostatic potential at the interfaces between two semiconductor segments is similar to that for semiconductor/insulator interfaces:
| (4.53) |
To calculate the carrier concentrations and the carrier temperatures at the interface, three different approaches are considered:
Each model can be specified for electrons and holes for each semiconductor/semiconductor interface.
In the following
![]() denotes the normal to the interface component of the
current density
denotes the normal to the interface component of the
current density
![]() ,
,
![]() the energy
flux density component, and
the energy
flux density component, and
![]() the difference in the
conduction band edges
the difference in the
conduction band edges
![]() . The effective electron mass is
denoted by
. The effective electron mass is
denoted by ![]() . The subscripts denote the semiconductor segment
. The subscripts denote the semiconductor segment
![]() . Only the equations for electrons are given, those for holes can
be deduced accordingly.
. Only the equations for electrons are given, those for holes can
be deduced accordingly.
Dirichlet boundary conditions are applied, when the CQFL is used. The
carrier concentrations are determined so that the quasi-Fermi levels
remains continuous across the interface [134].
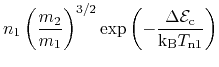 |
(4.54) | ||
| (4.55) | |||
| (4.56) | |||
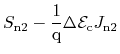 |
(4.57) |
To consider the band gap alignment as typical in a heterostructure, the
thermionic emission or thermionic field emission interface models must
be used.
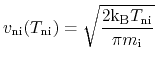 |
(4.62) |
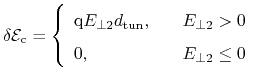 |
(4.63) |