4.4.1 Low-Field Mobility

Ionized Impurity Scattering:

The low-field mobility is modeled by an expression similar to that proposed by Caughey and Thomas [341,138]:

$$\mu^\ensuremath{\mathrm{LI}} = \mu^\ensuremath{\mathrm{min}} + \f... ...eft(C_\ensuremath{\mathrm{I}}/C^{\ensuremath{\mathrm{ref}}}\right)^{\gamma_0}}.$$

C $_\ensuremath{\mathrm{I}}$ denotes the concentration of ionized impurities, $\mu^\ensuremath{\mathrm{L}}$ is the mobility in undoped material, $\mu^\ensuremath{\mathrm{min}}$ is the mobility in highly doped material, limited by impurity scattering. The maximum ( $\mu^\ensuremath{\mathrm{L}}$) mobility, and minimum ( $\mu^\ensuremath{\mathrm{min}}$) mobility, and the parameters describing the mobility decrease with rising impurity concentration ( $C^\ensuremath{\mathrm{ref}}$ and $\gamma_0$) are calibrated against an extensive analysis of available MC simulations results and experimental data.

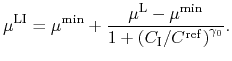For GaN our model for electrons assumes the high mobility consistent with the defect-free substrates of the simulated devices (Fig. 4.10). It is calibrated against own Monte Carlo simulation results presented in Section 3.2.2. The values of the parameters for GaN and other materials are given in Table 4.7.

Figure 4.10: Electron mobility versus concentration in GaN.

The model for electrons in InN is calibrated against own Monte Carlo (Fig. 4.11) simulation results, too, described in Section 3.3.2. The latter assumes an updated band gap of $\approx$0.7 eV and proper electron masses.

Figure 4.11: Electron mobility versus concentration in InN.

While for GaN and InN experimental data exist for the transport properties, for AlN such data are hardly available as the grown AlN films are normally semi-insulating. Most authors therefore rely on MC results [342]. We verified our model against the measurements of Taniyasu et al. [343] who achieved a high mobility in Si-doped AlN. They supplemented the experimental data with simulations (Fig. 4.12). The higher maximum mobility used here is in agreement with the value proposed in [253]. It is higher than the measured values, due to our model assumption of dislocation-free conditions.

Figure 4.12: Electron mobility versus concentration in AlN.

The hole transport in GaN is plagued by several doping technique issues as discussed in Section 3.2.3. Therefore, it is difficult to give a profound model. Based on the limited experimental data an initial setup is proposed (Fig. 4.13).

Figure 4.13: Hole mobility versus concentration in GaN.

Due to the lack of experimental data on the transport properties of holes in InN and AlN, no corresponding parameter setups are given here. Such can be found in [342], however solely based on Monte Carlo simulations.

The low field mobility of alloys is calculated by a harmonic mean:

$$\frac{1}{\mu^\ensuremath{\mathrm{ABC}}} = \frac{1-x}{\mu^\ensuremath{\mathrm{AC}}} + \frac{x}{\mu^\ensuremath{\mathrm{BC}}}.$$

Temperature Dependence:

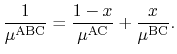In order to model the temperature dependence, the mobilities are parameterized using power laws [15]:

$$\mu^\ensuremath{\mathrm{L}} = \mu^\ensuremath{\mathrm{L}}_{300}\left(\ensuremath{\frac{\ensuremath{T_{\mathrm{L}}}}}{300 \ensuremath{\mathrm{K}}}\right)^{\gamma_1},$$

$$\mu^\ensuremath{\mathrm{min}} = \mu^\ensuremath{\mathrm{min}}_{300}\left(\ensuremath{\frac{\ensuremath{T_{\mathrm{L}}}}}{300 \ensuremath{\mathrm{K}}}\right)^{\gamma_2},$$

$$C^{\ensuremath{\mathrm{ref}}} = C^{\ensuremath{\mathrm{ref}}}_{300}\left(\ensuremath{\frac{\ensuremath{T_{\mathrm{L}}}}}{300 \ensuremath{\mathrm{K}}}\right)^{\gamma_3}.$$

Similar expressions have been also used by [253,175].

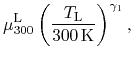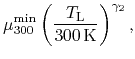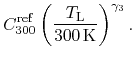Monte Carlo simulations by other groups [253,181] and experiments [345,346] for the electron mobility in bulk GaN as a function of the temperature are shown in Fig. 4.14. Over the years the electron mobilities increase due to the improved quality of the material samples. Models proposed by other groups [175,338] are also displayed. Fig. 4.15 shows the electron mobility as a function of temperature in the two-dimensional electron gas as experimentally determined by various groups [347,348,14,179,349,350]. The mobility exhibits overall higher values especially at high temperatures, while retaining the trend for improved results over time. The parameter values we chose are listed in Table 4.7. The maximum ( $\mu^\ensuremath{\mathrm{L}}_{300}$) and minimum mobility ( $\mu^\ensuremath{\mathrm{min}}_{300}$) are calibrated against own MC simulations. A decrease of the maximum mobility with temperature ( $\gamma_1=-1.5$), in agreement with the power term of the acoustic phonon mobility expression [110] is assumed. Our MC simulation results and recent experiments from [351] confirmed that the latter is the dominant scattering mechanism at high temperatures. A weak temperature dependence ( $\gamma_2=-0.2$) of the electron mobility at high concentrations is adopted.

Figure 4.14: Electron mobility versus temperature in bulk GaN.

Figure 4.15: Electron mobility versus temperature in 2DEG GaN.

Table 4.7: Parameter values for the low-field mobility.

Material	carrier	$\mu^\ensuremath{\mathrm{L}}_{300}$	$\mu^\ensuremath{\mathrm{min}}_{300}$	$C^\ensuremath{\mathrm{ref}}_{300}$	$\gamma_{0}$	$\gamma_{1}$	$\gamma_{2}$	$\gamma_{3}$
		[cm$^2$/Vs]	[cm$^2$/Vs]	cm$^{-3}$
GaN	n p	1600 175	100 10	3$\times$10$^{17}$ 2.5$\times$10$^{17}$	0.7 1.5	-1.5 -3.7	-0.2 -1.5	1.3 1.0
AlN	n	683	29	5$\times$10$^{17}$	0.8	-3.21	1.21	-0.18
InN	n	10200	500	3.4$\times$10$^{17}$	0.65	-3.7	2.39	-0.33

Experimental data for the mobility dependence on temperature for InN and AlN is scarce. Therefore, the values from [342] are adopted here.

The hole mobility at different temperatures of GaN is discussed in Section 3.2.3. Based on the experimental data, a value of $\gamma_1=-3.7$ is chosen which describes the decay in mobility with higher temperature well.