Subsections
4.4.3 High-Field Mobility for HD Equations
In order to obtain a consistent hydrodynamic mobility expression, the local energy balance equation:
is solved for
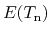 , which is then inserted into
(4.66). This is performed again with
, which is then inserted into
(4.66). This is performed again with 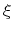 =1/2 for
both models, and with
=1/2 for
both models, and with 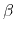 =2 for the first model and
=2 for the first model and 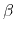 =1 for
the second model, respectively.
=1 for
the second model, respectively.
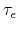 is the energy relaxation time.
is the energy relaxation time.
The expression obtained with the chosen values for 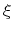 and
and 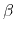 is
identical with the one proposed by Hänsch et al.
[356]. In order to account for NDM effects it is modified by
introducing two parameters (
is
identical with the one proposed by Hänsch et al.
[356]. In order to account for NDM effects it is modified by
introducing two parameters (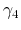 and
and 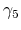 )
[20]:
)
[20]:
In the standard Hänsch model
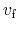 corresponds to the
saturation velocity
corresponds to the
saturation velocity
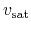 (as
in (4.66)). However, due to the powered temperature
term
(as
in (4.66)). However, due to the powered temperature
term
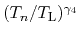 in the numerator the velocity is steadily
decreasing at high-fields. Hence,
in the numerator the velocity is steadily
decreasing at high-fields. Hence,
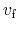 does not describe the
saturation velocity as a physical quantity, although it does affect
the high-field transport characteristics. The parameter
does not describe the
saturation velocity as a physical quantity, although it does affect
the high-field transport characteristics. The parameter 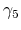 has
a more pronounced effect at low fields, while
has
a more pronounced effect at low fields, while 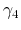 influences
primarily the high-field mobility, though their impact cannot be
isolated to a specific field region. The conventional Hänsch model
corresponds to the parameter set
influences
primarily the high-field mobility, though their impact cannot be
isolated to a specific field region. The conventional Hänsch model
corresponds to the parameter set
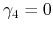 ,
,
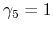 . However,
in order to approximate the simulation and experimental data, a set
with
. However,
in order to approximate the simulation and experimental data, a set
with
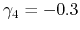 and
and
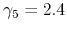 is chosen for GaN
(Table 4.10). It delivers good agreement with the
velocity-field characteristics obtained using the DD Model B
(Fig. 4.16). A similar good match with DD Model A can be
achieved for AlN, too (Fig. 4.17). Only for InN it is not
possible to model the very strong NDM effect.
is chosen for GaN
(Table 4.10). It delivers good agreement with the
velocity-field characteristics obtained using the DD Model B
(Fig. 4.16). A similar good match with DD Model A can be
achieved for AlN, too (Fig. 4.17). Only for InN it is not
possible to model the very strong NDM effect.
Table 4.10:
Parameters for HD high-field electron mobility Model A.
| |
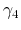 |
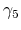 |
| Hänsch |
0.0 |
1.0 |
| GaN |
-0.3 |
2.4 |
| AlN |
0.1 |
3.3 |
Model B:
Inserting (4.72) into (4.66) with
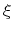 =1/2 and
=1/2 and 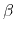 =2 gives the following expression for the
high-field mobility:
=2 gives the following expression for the
high-field mobility:
In order to approximate the intervalley transfer at high fields, two
sets of
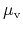 are used as in DD Model B. In this model too,
are used as in DD Model B. In this model too,
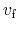 does not denote the saturation velocity. The weighted mean
is built:
does not denote the saturation velocity. The weighted mean
is built:
 |
(4.79) |
The expression for
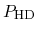 is analogous to that for
is analogous to that for
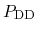 :
:
Fig. 4.19 compares the valley occupancy as a function of
the electric field as calculated in this model and MC simulation in
GaN. The used parameter setup is the same as for DD Model B
(Table 4.9). The only additional values needed, are the
scaled energy relaxation times listed in Table 4.11 (the
base relaxation times
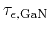 ,
,
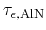 , and
, and
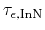 are
discussed in Section 4.4.4. An excellent agreement between
all models is achieved for GaN (Fig. 4.16). For InN the
model can describe the abrupt decay in velocity very well
(Fig. 4.18), while the maximum velocity value is slightly
higher than the one achieved by the DD model (which is possibly due to
the high energy relaxation times used).
are
discussed in Section 4.4.4. An excellent agreement between
all models is achieved for GaN (Fig. 4.16). For InN the
model can describe the abrupt decay in velocity very well
(Fig. 4.18), while the maximum velocity value is slightly
higher than the one achieved by the DD model (which is possibly due to
the high energy relaxation times used).
Figure 4.19:
GaN valley occupancy as a function of the electric field.
|
![\includegraphics[width=10cm]{figures/models/mobility/Pop2.eps}](img525.png) |
While the models deliver consistent results, the two approaches expose
some differences. HD Model A is close to already established models
and offers a straightforward calibration with only two auxiliary
parameters (within a narrow value range). HD Model B is more complex,
however, it allows for a more flexible calibration. Its parameters are
derived from physical quantities.
Table 4.11:
Parameters for the energy relaxation times for HD high-field
electron mobility Model B [ps].
| |
 |
 |
| GaN |
8.0
 |
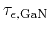 |
| InN |
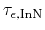 |
0.1
 |
S. Vitanov: Simulation of High Electron Mobility Transistors
![]() and
and ![]() is
identical with the one proposed by Hänsch et al.
[356]. In order to account for NDM effects it is modified by
introducing two parameters (
is
identical with the one proposed by Hänsch et al.
[356]. In order to account for NDM effects it is modified by
introducing two parameters (![]() and
and ![]() )
[20]:
)
[20]:
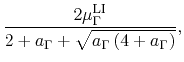



![]() are used as in DD Model B. In this model too,
are used as in DD Model B. In this model too,
![]() does not denote the saturation velocity. The weighted mean
is built:
does not denote the saturation velocity. The weighted mean
is built:
