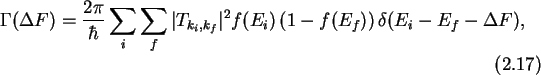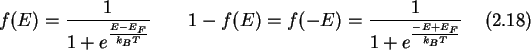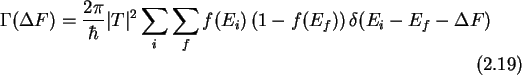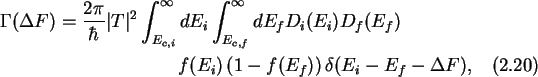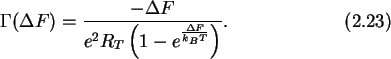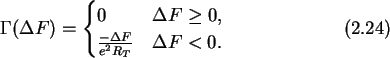Next: 2.5 Minimum Tunnel Resistance
Up: 2.4 Tunneling
Previous: 2.4.1 Transmission Probability
2.4.2 Tunnel Rate
The tunnel rate from an initial state i to a final state f, considering
the change in free energy and using
Fermi's golden rule
(Appendix E), is expressed as [53]
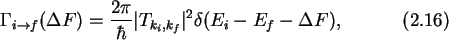
where
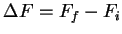 is the difference in final and initial free energy.
Hence a transition to a state with lower
free energy produces a negative change in free energy.
The difference of initial energy Ei and final energy Ef of the
tunneling electron
has to account for the change in free energy its transition causes. The
total tunnel rate from occupied states on one side of the
barrier to
unoccupied states on the other side of the barrier is given by the
expression
is the difference in final and initial free energy.
Hence a transition to a state with lower
free energy produces a negative change in free energy.
The difference of initial energy Ei and final energy Ef of the
tunneling electron
has to account for the change in free energy its transition causes. The
total tunnel rate from occupied states on one side of the
barrier to
unoccupied states on the other side of the barrier is given by the
expression
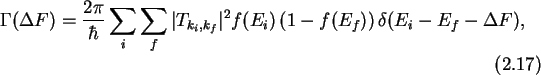
where f(E) is the Fermi-Dirac distribution,
or Fermi function which gives
the occupation probability of
energy levels. (1-f(E)) is therefore the
probability of finding an empty state.
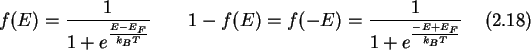
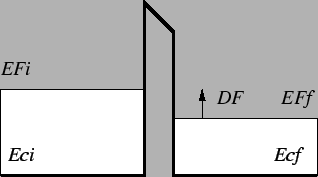
For a typical metal tunnel junction, the barrier
consists of a thin oxide
with a relatively high barrier height (see
Fig. 2.5).
Figure 2.5:
Tunnel barrier.
 |
It is usually a reasonable approximation for such cases to
neglect the variation of the tunnel
transmission coefficient with energy and momentum. The transmission
probability |T|2 can then be treated as a constant which may be taken
outside of the summation of (2.17).
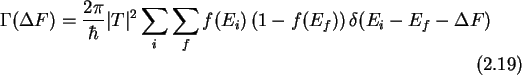
Using the density of states D(E), the number of electron states in
a small energy interval dE is given by 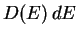 .
This can be used to
convert the sums over momentum in (2.19) to integrals over
energy.
.
This can be used to
convert the sums over momentum in (2.19) to integrals over
energy.
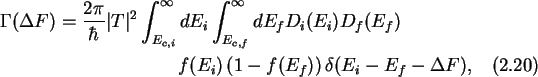
where Ec,i is the conduction band edge of
the side where the electron
resides initially, Ec,f is the conduction band edge of the side the
electron is tunneling to, the final side, Di(E) is the
density of states on the initial side and
Df(E) is the density of states of the final side of the potential barrier.
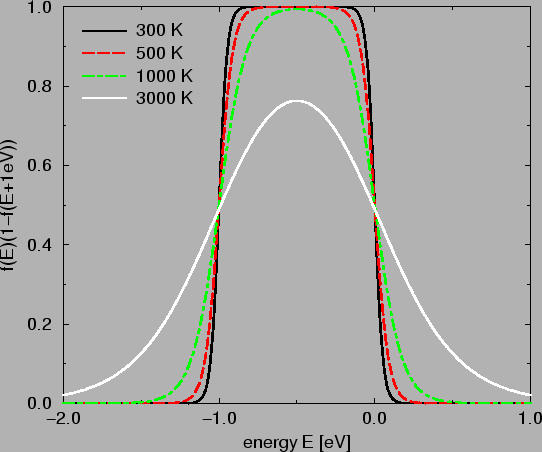
The product of the two Fermi functions
defines an almost rectangular window around the Fermi energies of initial
and final side (see Fig. 2.6).
Figure 2.6:
The product of the two Fermi functions defines for the
interesting temperatures (around 300 K) an almost rectangular window.
EFi - EFf =1 eV.
 |
Since the main contribution of the integral comes from this narrow window,
the densities of states appearing in the integral may be taken constant and
moved in front of the integral as well. The delta function reduces one of
the integrations such that
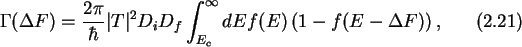
where the lower limit of the integration is the higher of the two conduction
band minima
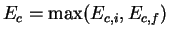 .
Neglecting charging effects, a tunnel junction
has an Ohmic
IV-characteristic.
Which means that the current through the
junction is proportional to the applied bias voltage across the junction.
Therefore the phenomenological quantity
`tunnel resistance' can be
introduced [25], I=V/RT. The tunnel resistance incorporates
the transmission probability and the density of states.
.
Neglecting charging effects, a tunnel junction
has an Ohmic
IV-characteristic.
Which means that the current through the
junction is proportional to the applied bias voltage across the junction.
Therefore the phenomenological quantity
`tunnel resistance' can be
introduced [25], I=V/RT. The tunnel resistance incorporates
the transmission probability and the density of states.
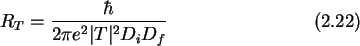
Inserting (2.22) in (2.21) and using
the properties of the Fermi function (see Appendix D,
especially (D.5))
one gets the main result of the `orthodox' single-electron tunnel
theory
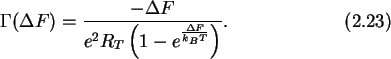
For zero temperature this reduces to
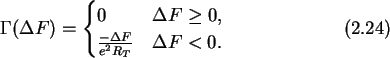




Next: 2.5 Minimum Tunnel Resistance
Up: 2.4 Tunneling
Previous: 2.4.1 Transmission Probability
Christoph Wasshuber