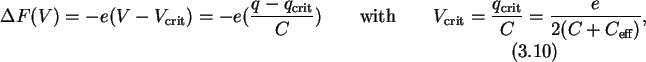Next: 3.2 Tunneling: a Stochastic
Up: 3.1 Free Energy of
Previous: 3.1.4 Free Energy
3.1.5 Method of Critical Voltage
The first term for the calculation of the change in free energy in
(3.8) is a quadratic form, a vector-matrix-vector
multiplication which needs 2N2-1 scalar operations (multiplications
and additions) for its evaluation. It is possible to reduce this expenditure
slightly
to 2N2-N-1 operations by employing the method of critical voltage or
critical charge [28] [38] [46] [97].
Since this is only a linear reduction for a quadratic expression it will not
matter much for large circuits. However the concept of a critical charge,
as is shown in the following, may help in understanding the operation of
more complex circuits.
Asking what free energy change a tunnel event in a particular junction
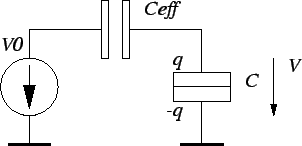
causes, one may look at the equivalent circuit Fig. 3.4 using
Thévenin's theorem.
Figure 3.4:
Thévenin equivalent circuit of a tunnel junction. The circuit
surrounding the tunnel junction is reduced into the effective capacitance and
the voltage source.
 |
The change in free energy, which includes electrostatic energy and
work done by the voltage source, may be written as a linear function of the
voltage across the tunnel junction V, or, what is equivalent, as a function
of the charge q on the tunnel junction.
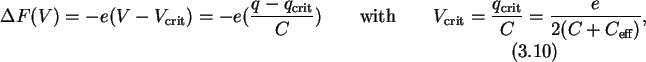
where
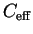 is the
effective
capacitance of the Thévenin
equivalent circuit.
The critical voltage is computed once for every junction outside the inner
simulation loop. In the inner loop only node potentials are calculated
(3.2), which is a matrix-vector multiplication, from which the
voltage across tunnel junctions and finally, using the critical voltage, the
change in free energy (3.10) is calculated. Studying
the changing voltage across a tunnel junction in comparison to the constant
critical voltage may lead to a better understanding when tunnel rates
are likely and when not. It is possible to use the critical voltage as the
basis to the determination of stable and
instable regions of device
operation [97]. For zero temperature (3.10) gives
the region where tunneling is allowed as
is the
effective
capacitance of the Thévenin
equivalent circuit.
The critical voltage is computed once for every junction outside the inner
simulation loop. In the inner loop only node potentials are calculated
(3.2), which is a matrix-vector multiplication, from which the
voltage across tunnel junctions and finally, using the critical voltage, the
change in free energy (3.10) is calculated. Studying
the changing voltage across a tunnel junction in comparison to the constant
critical voltage may lead to a better understanding when tunnel rates
are likely and when not. It is possible to use the critical voltage as the
basis to the determination of stable and
instable regions of device
operation [97]. For zero temperature (3.10) gives
the region where tunneling is allowed as
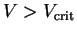 .
V usually
is a function of some external gate and bias voltage sources. Then
.
V usually
is a function of some external gate and bias voltage sources. Then
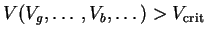 defines a border between
a stable and an instable region. In general the border is an n-dimensional
plane, with n being the number of independent quantities V is depending
on. Every tunnel junction defines such a plane. Altogether they mark
regions of stable and instable operation.
defines a border between
a stable and an instable region. In general the border is an n-dimensional
plane, with n being the number of independent quantities V is depending
on. Every tunnel junction defines such a plane. Altogether they mark
regions of stable and instable operation.




Next: 3.2 Tunneling: a Stochastic
Up: 3.1 Free Energy of
Previous: 3.1.4 Free Energy
Christoph Wasshuber