



Next: 3.3 Master Equation Method
Up: 3 Simulation of Single
Previous: 3.1.5 Method of Critical
3.2 Tunneling: a Stochastic Process
Quantum mechanics tells us the transmission probability and rate of one
electron tunneling through a potential barrier, but has little to say about
the statistics of many electrons tunneling. To make statements about the
many body problem
a single-electron circuit represents, one has to include the formalism of statistical
mechanics and stochastic processes. One can only
speculate about the statistics governing tunneling. Nevertheless, the model
discussed below gives very good experimental agreement, which confirms the
model's soundness.
The first assumption is that electrons can not probe the past, that is they
posses no memory, and thus their tunnel rate depends only on the
momentary state of the system. This is exactly the
criterion for a Markov process [100]. If one
further assumes, that
the system evolves at random times in a jump like fashion, as is the case
with tunneling, one can describe such a system with a
ME [37]
![\begin{gather}
\frac{\partial p(\boldsymbol{S},t)}{\partial t}=\int d\boldsymbol...
...mma(\boldsymbol{S'}\vert\boldsymbol{S}) p(\boldsymbol{S},t)\right],
\end{gather}](img209.gif)
where
p(S,t) is the probability density function in state space, and
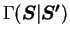 denotes the transition rate from state
S'
to state
S. If the states are discrete the ME becomes
denotes the transition rate from state
S'
to state
S. If the states are discrete the ME becomes
![\begin{gather}
\frac{\partial P_i(t)}{\partial t} = \sum_{j\neq i} \left[\Gamma_{ij}P_j(t) -
\Gamma_{ji}P_i(t)\right],
\end{gather}](img210.gif)
where
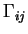 denotes the transition rate from state j to state iand Pi(t) is the time dependent
occupation
probability of state i.
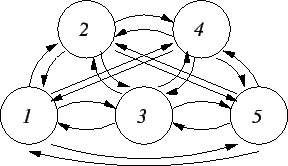
Fig. 3.5 is a typical state transition diagram for such a
process.
denotes the transition rate from state j to state iand Pi(t) is the time dependent
occupation
probability of state i.
Fig. 3.5 is a typical state transition diagram for such a
process.
Figure 3.5:
State transition diagram for a jump process with five discrete
states.
 |
The ME method for the simulation of SET circuits tries to solve
(3.12) which is the general description of a SET circuit,
numerically, as was done by L. Fonseca et al. [32].
Taking the simplification one step further and
considering only a single tunnel junction, where the number
of tunneled electrons gives the state of the
system, the state can only change to a neighboring state, since
only one electron is assumed to tunnel at a time. Processes with this
property are called point or
birth-death processes [52] and
can be visualized with a simple state
transition diagram
Fig. 3.6.
Figure 3.6:
State transition diagram of a point or birth-death process.
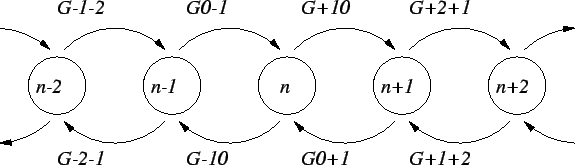 |
Further assuming that states can only evolve in one direction, this is the
case if only tunneling in one direction is considered, and that all states
have an equal transition rate to the next state, which is the case when
neglecting any charging effects, brings one to the so called
Poisson process,
Fig. 3.7.
Figure 3.7:
State transition diagram of a Poisson process.
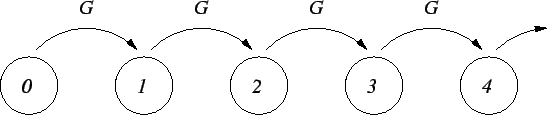 |
The Poisson process starts at n=0 and evolves monotonously to higher state
numbers. The transition rate is the same for every state.
The ME for the Poisson process is
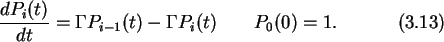
This first order differential equation with constant coefficients may
be solved by Laplace transforming both sides.

where
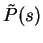 is the Laplace transform of P(t).
Using the initial conditions P0(0)=1 and
Pi>0(0)=0 gives
is the Laplace transform of P(t).
Using the initial conditions P0(0)=1 and
Pi>0(0)=0 gives
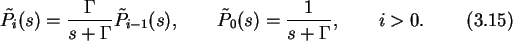
This set of recursive equations for the state probability Laplace transform
is easily solved by induction.
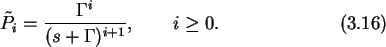
Taking the inverse Laplace transform, one finds that for 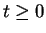 and
and
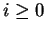 ,
,

This is the well known Poisson distribution.
Building on the stochastic
description of a single tunnel junction with the Poisson process, it is
possible to use a MC method for the simulation of SET circuits.




Next: 3.3 Master Equation Method
Up: 3 Simulation of Single
Previous: 3.1.5 Method of Critical
Christoph Wasshuber
![\begin{gather}
\frac{\partial P_i(t)}{\partial t} = \sum_{j\neq i} \left[\Gamma_{ij}P_j(t) -
\Gamma_{ji}P_i(t)\right],
\end{gather}](img210.gif)
![]()
![]() denotes the transition rate from state
S'
to state
S. If the states are discrete the ME becomes
denotes the transition rate from state
S'
to state
S. If the states are discrete the ME becomes
![\begin{gather}
\frac{\partial P_i(t)}{\partial t} = \sum_{j\neq i} \left[\Gamma_{ij}P_j(t) -
\Gamma_{ji}P_i(t)\right],
\end{gather}](img210.gif)
![]() denotes the transition rate from state j to state iand Pi(t) is the time dependent
occupation
probability of state i.
Fig. 3.5 is a typical state transition diagram for such a
process.
denotes the transition rate from state j to state iand Pi(t) is the time dependent
occupation
probability of state i.
Fig. 3.5 is a typical state transition diagram for such a
process.