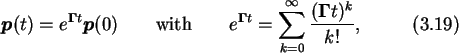Next: 3.3.1 Krylov Subspace Approximate
Up: 3 Simulation of Single
Previous: 3.2 Tunneling: a Stochastic
The ME method tries to solve (3.12). The main problem of the
ME method is to obtain the set of relevant states the circuit under
investigation can occupy. The states and their transition rates bring about
the circuit describing differential equations which may be written in
matrix form for n states as
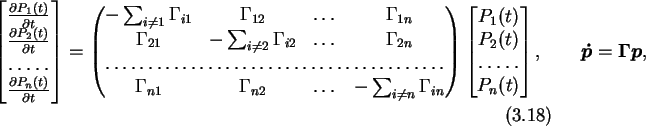
where
p is the vector of state probabilities
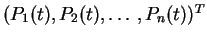 .
SET circuits with islands have an infinite number of states, because the
number of excess electrons is unbound. Clearly higher numbers of excess
carriers are due to the Coulomb blockade exponentially suppressed and become more and
more unlikely. But it is almost impossible to filter out a priori the most
likely states from an arbitrary circuit. The most sensible approach is
an adaptive scheme where one starts with the initial state, calculates
rates for all possible transitions and uses these rates as a zero-order
estimate for the state probability. High transition rates will lead in
general to a
state with high probability and vice versa. If the rate falls below a
threshold the state will not be considered. Then the ME is solved
with all states that passed the threshold test. In the next iterations new
states will join the set of relevant states and the circuit will be described
better and better. This iterative method may be pictured as a journey in
state space. Starting at the set of states already found, which is for the
first iteration only the initial state, one step is made at a time starting
from every state of the set. These steps may lead to states that are already
in the set, or to new states. The rate to the new state determines if it
should be taken in the set of relevant states or not.
.
SET circuits with islands have an infinite number of states, because the
number of excess electrons is unbound. Clearly higher numbers of excess
carriers are due to the Coulomb blockade exponentially suppressed and become more and
more unlikely. But it is almost impossible to filter out a priori the most
likely states from an arbitrary circuit. The most sensible approach is
an adaptive scheme where one starts with the initial state, calculates
rates for all possible transitions and uses these rates as a zero-order
estimate for the state probability. High transition rates will lead in
general to a
state with high probability and vice versa. If the rate falls below a
threshold the state will not be considered. Then the ME is solved
with all states that passed the threshold test. In the next iterations new
states will join the set of relevant states and the circuit will be described
better and better. This iterative method may be pictured as a journey in
state space. Starting at the set of states already found, which is for the
first iteration only the initial state, one step is made at a time starting
from every state of the set. These steps may lead to states that are already
in the set, or to new states. The rate to the new state determines if it
should be taken in the set of relevant states or not.
The stationary case of (3.18),
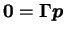 ,
is a system of linear equations which may be solved by a multitude of
numerical algorithms [44]. The transient case which is a system of
ordinary linear first order homogeneous differential equations, may be
solved either by formally integrating (3.18)
,
is a system of linear equations which may be solved by a multitude of
numerical algorithms [44]. The transient case which is a system of
ordinary linear first order homogeneous differential equations, may be
solved either by formally integrating (3.18)
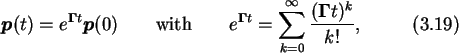
and calculating the exponential of a matrix, or by solving the system of
differential equations without explicitly forming the exponential of the
transition rate matrix. For taking the exponential of a matrix the
rational Padé approximation is one of the
better algorithms available
[44] [100]. Nevertheless, a major disadvantage of Padé
approximants is
that they are accurate only near the origin and so should not be used when
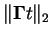 is large. One can assure the smallness of the norm
by making t accordingly small. This means that the time discretisation might
become inconveniently small. A description of rational Padé approximation
is given in Appendix G. For the solution of ordinary differential
equations a wide variety of methods exist, such as Euler, Taylor series,
Runge-Kutta, single-step, and multi-step methods [48] [49].
Most methods experience difficulty if
is large. One can assure the smallness of the norm
by making t accordingly small. This means that the time discretisation might
become inconveniently small. A description of rational Padé approximation
is given in Appendix G. For the solution of ordinary differential
equations a wide variety of methods exist, such as Euler, Taylor series,
Runge-Kutta, single-step, and multi-step methods [48] [49].
Most methods experience difficulty if
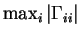 ,
the largest
exit rate from any state, and t, the time interval in which the solution is
required, are large. Only the relatively novel approach of using Krylov
subspaces is promising over a large range of parameters, since this method
isolates the eigenvalues which dominate the matrix exponential. Therefore we
outline the basic Krylov subspace method in more detail.
,
the largest
exit rate from any state, and t, the time interval in which the solution is
required, are large. Only the relatively novel approach of using Krylov
subspaces is promising over a large range of parameters, since this method
isolates the eigenvalues which dominate the matrix exponential. Therefore we
outline the basic Krylov subspace method in more detail.




Next: 3.3.1 Krylov Subspace Approximate
Up: 3 Simulation of Single
Previous: 3.2 Tunneling: a Stochastic
Christoph Wasshuber