



Next: 3.5 Comparison between Master
Up: 3 Simulation of Single
Previous: 3.3.1 Krylov Subspace Approximate
To use the MC method for the simulation of SET circuits was
first proposed and implemented by N. Bakhvalov et al. [13]. Other
groups adopted this method later [18] [61] [97].
From (3.17), the probability that a tunnel event
out of state 0 happens at 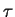 and not earlier is
and not earlier is

To construct random numbers which are distributed like
(3.28), from evenly distributed random numbers, one has
to take the inverse of the distribution function [58].

where r is an evenly distributed random number from the interval
]0,1[. The MC procedure is then as follows. Starting from all possible
tunnel events with their particular tunnel rates, concrete tunnel times
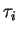 are computed according to (3.29). The event
with the smallest
are computed according to (3.29). The event
with the smallest 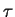 will happen first and thus is taken as the
winner of the MC method. Node charges are updated according to the so
computed tunnel event, which further brings changing node potentials in its
train. New tunnel rates are calculated and a new winner is determined through
MC simulation. Doing this many times gives the macroscopic behavior of
the circuit. Another possibility is to calculate first an exit tunnel time
out of the current state k,
will happen first and thus is taken as the
winner of the MC method. Node charges are updated according to the so
computed tunnel event, which further brings changing node potentials in its
train. New tunnel rates are calculated and a new winner is determined through
MC simulation. Doing this many times gives the macroscopic behavior of
the circuit. Another possibility is to calculate first an exit tunnel time
out of the current state k,
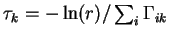 ,
and
selecting afterwards with a second random process, which event it was.
One or the other scheme will have a shorter run time, depending on how
long the evaluation of a logarithm and the generation of an evenly
distributed random number takes.
,
and
selecting afterwards with a second random process, which event it was.
One or the other scheme will have a shorter run time, depending on how
long the evaluation of a logarithm and the generation of an evenly
distributed random number takes.




Next: 3.5 Comparison between Master
Up: 3 Simulation of Single
Previous: 3.3.1 Krylov Subspace Approximate
Christoph Wasshuber