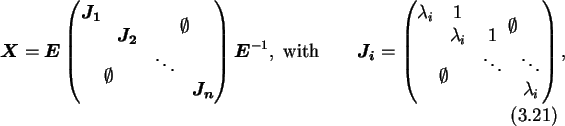
where Ji are the Jordan blocks and
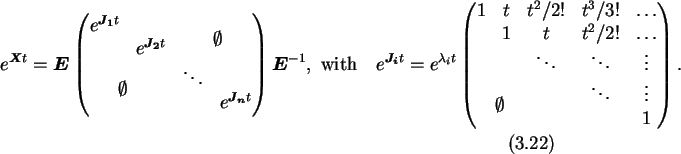
A particular decomposition is the Jordan
canonical form which is for a matrix
X
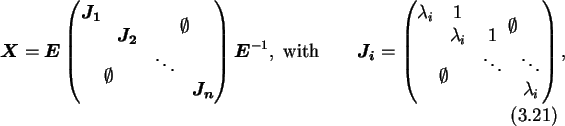
where
Ji are the Jordan blocks and ![]() are the eigenvalues of
X. A Jordan block
Ji has typically a dimension of one. This
is the case if the algebraic multiplicity and the geometric multiplicity of
are the eigenvalues of
X. A Jordan block
Ji has typically a dimension of one. This
is the case if the algebraic multiplicity and the geometric multiplicity of
![]() are equal. Otherwise
the dimension of the Jordan block increases by the difference of
algebraic to geometric multiplicity. If all Jordan blocks have dimension one
the matrix is said to be non-defective or diagonalizable.
Using the Jordan canonical form the
exponential of
Xt is given by
are equal. Otherwise
the dimension of the Jordan block increases by the difference of
algebraic to geometric multiplicity. If all Jordan blocks have dimension one
the matrix is said to be non-defective or diagonalizable.
Using the Jordan canonical form the
exponential of
Xt is given by
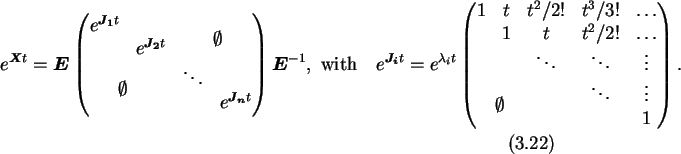
One needs to calculate the exponential of the transition rate matrix
![]() (see(3.19)). Due to the special structure of
(see(3.19)). Due to the special structure of
![]() with main diagonal elements
with main diagonal elements
![]() it can be shown by Gershgorin's
circle theorem that all its eigenvalues lie in the left half-plane and one
eigenvalue is zero (see left side of Fig. 3.8).
it can be shown by Gershgorin's
circle theorem that all its eigenvalues lie in the left half-plane and one
eigenvalue is zero (see left side of Fig. 3.8).
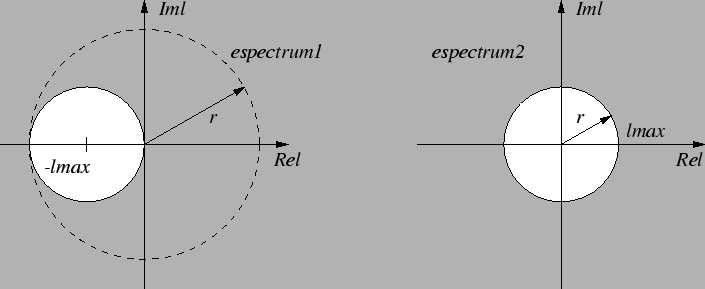 |
The transformed matrix
![]() has its eigenvalues which
dominate the exponential function in the outermost part of its spectrum.
Thus, a Krylov subspace method will give good results even for small
dimension subspaces.
has its eigenvalues which
dominate the exponential function in the outermost part of its spectrum.
Thus, a Krylov subspace method will give good results even for small
dimension subspaces.
The objective is the computation of an approximation of the form
![]() to the matrix exponential operation
to the matrix exponential operation
![]() ,
where
,
where
![]() is a
polynomial
of degree m-1 in
is a
polynomial
of degree m-1 in
![]() ,
which is a linear combination of the
vectors
,
which is a linear combination of the
vectors
![]() ,
and thus is an element of the Krylov subspace [98]
,
and thus is an element of the Krylov subspace [98]
![]()
Constructing an orthonormal basis
![]() in the Krylov subspace,
and choosing
in the Krylov subspace,
and choosing
![]() ,
one may write using the
identity
BmBmT=I
,
one may write using the
identity
BmBmT=I
![]()
where
e1 is the unit vector
![]() .
The purpose of the
Krylov subspace approach, namely to project the exponential of a large
matrix approximately onto a small Krylov subspace, is accomplished by
approximating
.
The purpose of the
Krylov subspace approach, namely to project the exponential of a large
matrix approximately onto a small Krylov subspace, is accomplished by
approximating
![]() with
with
![]() .
This gives the
approximation
.
This gives the
approximation
![]()
which still involves the evaluation of the exponential of a matrix, but this
time of small dimension m and of a particular structure, namely upper
Hessenberg.
Bm and
Hm can be computed by the Arnoldi algorithm
(see Appendix H), which is a modified Gram-Schmidt
orthogonalization. Y. Saad [98] shows that an a priori error bound
exists.
![]()