Step Size

   An ideal random number generator for uniformly distributed numbers should be able to generate any real number from its interval, for instance, [0,1]. However, due to the finite precision storage of real numbers in computers, random number generators will exhibit a finite step size in their generated numbers. The step size of a random number generator gives the maximum length of an interval out of all intervals in which the generator cannot generate any random number. 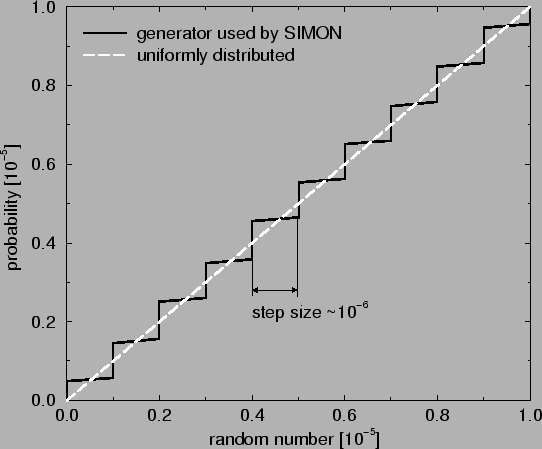The multiple linear congruential method which SIMON uses has a step size of 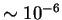$\sim 10^{-6}$, as shown in Fig. 4.8 which plots the probability function (4.6). Fig. 4.8 shows only the interval [0,10^-5], however, a similar structure is found in the whole interval [0,1].

  

Figure 4.8: Resolution limit of random generators.

From this step size a measure for the    resolution limit of the MC method may be derived. Resolution means the ratio of the tunnel rate of the rarest to the most frequent event. Considering (3.29), we ask what is the shortest duration between two tunnel events of the rarest process and what is the longest duration of the most frequent tunnel process.
$$\begin{gather}\tau_{\text{max,frequent}} = -\frac{\ln(10^{-6})}{\Gamma_{\text{fr... ...}}% {\Gamma_{\text{frequent}}} > \frac{10^{-6}}{14} \approx 10^{-7} \end{gather}$$
That means if rare and frequent tunnel events occur at the same time, for instance one part of the circuit is in a Coulomb blockade and only the rare co-tunneling process takes place and the other part shows normal tunneling, only events smaller by a factor 10⁷ as the most frequent event will be simulated. Other events will never come out as the winner of the MC simulation, because their tunnel duration is too long. However, if the whole circuit is in a Coulomb blockade this limitation does not apply and much rarer events will be resolved.