



Next: Step Size
Up: 4.2 Code structure
Previous: 4.2.2 Flow Chart
The heart of a MC method is the
pseudo random number generator.
Simulation results are only as good as the pseudo random numbers (PRN) satisfy
certain statistical properties. PRN are derived deterministically. However,
they still can exhibit features, such as mean value, variance and
standard deviation, of a truly random sequence. If not desired systematic
dependences
between the generated numbers exist, simulation results will reflect
these dependences which are only artifacts of the random number generation,
which have nothing to do with the circuit that should be simulated. Clearly,
this has to be avoided.
H. Niederreiter [91] distinguishes three groups of
PRN-generators: linear congruential generators, nonlinear congruential
generators, and shift-register generators.
Probably the most popular method for
uniformly distributed PRN is the
linear
congruential method [62].
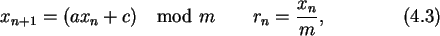
where m, a, and c are three parameters which determine the quality of
the generated numbers. Clearly the maximum period of the pseudo-random
number sequence is m. Thus m will usually be chosen close to the maximum
integer number representable in a single register of the processor. The
other two parameters a and c should be relatively prime to m.
The linear congruential method has the advantage of being very fast,
requiring only a few operations per call. It has the disadvantage that
it is not free of sequential correlation on successive calls. Thus for
SIMON we are using a random generator that
shuffles
the output of a
linear congruential method to remove the least significant bit correlations
[96]. To achieve the shuffling, a computed random number rn is not
output as the n-th random number, but rather at a randomized later
call.
Another derivative of a linear congruential method is a
nonlinear
congruential method, of which the inversive congruential method is a special
case.
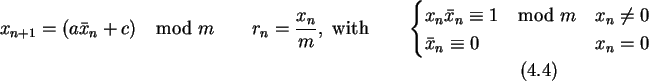
The
inversive
congruential method has superior statistical properties
compared to the plain linear congruential method [91]. On the
other hand the
calculation of 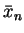 for a given xn consumes additional
computational resources and thus this method is not so efficient. The
Euclidean algorithm to calculate
for a given xn consumes additional
computational resources and thus this method is not so efficient. The
Euclidean algorithm to calculate 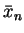 for a given xn from
[62] terminates in average after
for a given xn from
[62] terminates in average after
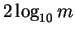 steps.
steps.
The
shift-register generators
received their name from the fact, that such
generators can be built in hardware from shift registers with a
feedback. If m is a small prime, usually m=2, a shift-register
method can be written as
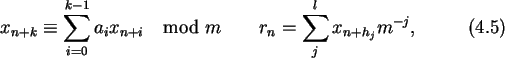
with 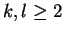 and integers
and integers
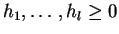 .
In the case of m=2shift-register generators can be implemented efficiently since only binary
arithmetic is needed. They too have better statistical properties than a
simple linear congruential method.
.
In the case of m=2shift-register generators can be implemented efficiently since only binary
arithmetic is needed. They too have better statistical properties than a
simple linear congruential method.
A complicated computation of random numbers does not necessarily
guarantee their randomness. In the contrary the more complicate the harder
it is to derive theoretical justifications for the soundness of the method.
However, the only way to guarantee the quality of a random generator is
thorough testing. One test for the accuracy of the probability distribution
of the PRN is to plot their probability function

where p(r) is the probability distribution of the PRN. The function F(x)
gives
the probability that the random number r is smaller than x.
Fig. 4.6 compares F(x) for x<10-4 for the
above explained random generator that SIMON uses and a simple linear
congruential method with the parameters
(m,a,c)=(714025,1366,150889).
Figure 4.6:
Comparison of two uniformly distributed random number generators.
The first 10000 random numbers that fell into the shown interval were
taken to generate the plot.
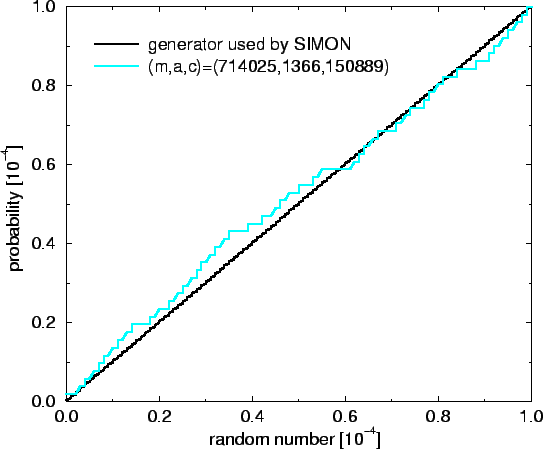 |
The simple linear congruential method shows deviations to the ideal
characteristic F(x)=x, and bigger steps in the fine structure.
Fig. 4.6 shows only the interval [0,10-4],
however, a similar behavior is found in the remaining part
[10-4,1].
The lattice structure is another important property
of PRN-generators [91].
The presence of a regular lattice structure can be assessed by looking at
points
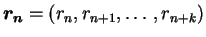 .
In the case of linear
congruential methods all
rn lie on relatively few parallel
hyperplanes, as is shown on the left side of Fig. 4.7.
.
In the case of linear
congruential methods all
rn lie on relatively few parallel
hyperplanes, as is shown on the left side of Fig. 4.7.
Figure 4.7:
Lattice structure of the first 5000 successive random numbers of two
random sequences. The left was generated by the linear congruential method
(m,a,c)=(6075,106,1283), the other is the shuffled congruential method
used in SIMON. The simple linear congruential method on the left side exhibits
a regular lattice structure where all points lie on parallel hyperplanes.
In the middle part of the lattice the hyperplanes are explicitly shown.
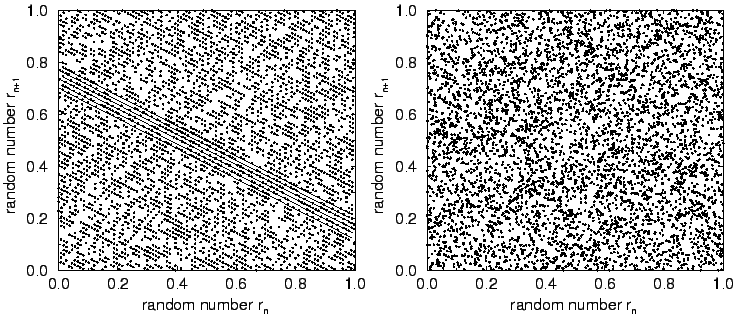 |
In comparison the right side shows points for the shuffled congruential
method used in SIMON. There such parallel hyperplanes are not visible.




Next: Step Size
Up: 4.2 Code structure
Previous: 4.2.2 Flow Chart
Christoph Wasshuber
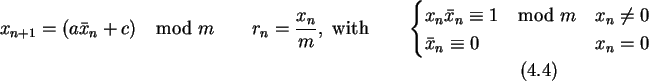
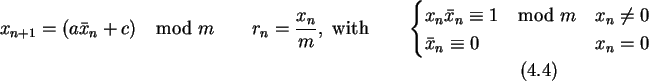
![]() for a given xn consumes additional
computational resources and thus this method is not so efficient. The
Euclidean algorithm to calculate
for a given xn consumes additional
computational resources and thus this method is not so efficient. The
Euclidean algorithm to calculate ![]() for a given xn from
[62] terminates in average after
for a given xn from
[62] terminates in average after
![]() steps.
steps.
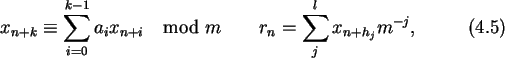
![]() and integers
and integers
![]() .
In the case of m=2shift-register generators can be implemented efficiently since only binary
arithmetic is needed. They too have better statistical properties than a
simple linear congruential method.
.
In the case of m=2shift-register generators can be implemented efficiently since only binary
arithmetic is needed. They too have better statistical properties than a
simple linear congruential method.
![]()

