5.2.11 Discussion of Simulation Results

  We studied the dependences on the operation temperature and on the random background charge of the six memory designs by simulation. We did not set an error limit to define the operation temperature, but measured at which temperature the functioning of the memory stops. Usually this point is very pronounced. Raising the temperature produces more and more errors until the desired behavior vanishes. The maximum temperature given in Table 5.1 is to be understood as the maximum operation temperature achievable with a characteristic capacitance of 0.35 aF. Reducing the size of the tunnel junctions and thus also their capacitance, will shift all operation temperatures accordingly to higher values and vice versa. The dependence on random background charge was measured at half the maximum operation temperature. For the simulations done here all capacitances are 0.35 aF and all tunnel resistances are $10^{5}\ \Omega$, if not stated otherwise.

As one can see in Table 5.1 the straight forward copy of conventional design, as was done with the flip-flop, is the worst choice.

The operation temperature is low, because the capacitors C₀ which cross connect both inverters have to be about a factor three bigger than the capacitance of the tunnel junctions. This increases the capacity of the quantum dots. The next best choice is the ring memory, ring-trap memory or MTJ memory. All three are similar in design idea. But the MTJ memory has twice as high an operation temperature. This can be understood as follows. To introduce an error in the MTJ memory, at least one electron has to tunnel from the quantum dot QD all the way to ground. That is, it has to pass six tunnel junctions in our example. In the case of the ring memory two electrons have to tunnel only through a single junction to change the state of the cell, because once two electrons tunneled in the same direction it is energetically favorable for the third electron to tunnel too. Thus the MTJ memory has a bigger barrier against thermal fluctuations. In the case of ring-trap memory thermal fluctuations introduce charge oscillations even when no electrons are stored in the ring. This could trigger Coulomb oscillations in the read-out SET transistor. That is why the operation temperature is equal to the ring memory. However the read-out circuit can be improved, by adding a filter. Thermal fluctuations are uncorrelated, but the charge shifts due to a pulsed read-out voltage $V_{\text{read}}$ have a specific frequency which could be filtered out. With this added complexity the operation temperature should be improved considerably.

 

Table: Comparison of maximum operation temperature T_max, random background charge dependence, and of the complexity of six memory designs. The simulations were done with tunnel junction capacitances of 0.35 aF and tunnel resistances of 100k$\Omega$.

memory design	$T_{\text {max}}$	Q0-dependence	number of elements
flip-flop	17 K	yes	10-14
multi-tunnel-junction memory	74 K	yes	7
ring memory	34 K	yes	12
ring-trap memory	34 K	no	13
Q0-independent memory	315 K	no	4
multi-island memory	86 K	no	NA

 

Flip-flop, MTJ memory, and ring memory are very sensitive to random background charge. Therefore, as long as the available process technology cannot provide impurity free materials, these designs are of no practical value today. The ring-trap memory, Q₀-independent memory, and the multi-island memory are very interesting alternatives. All three are independent of random background charge. The Q₀-independent memory has a big advantage in operation temperature. The reason is, that the Coulomb oscillations are visible at much higher temperatures than a clear Coulomb blockade. On the other hand, the multi-island memory is simpler in structure and allows non-destructive readout.

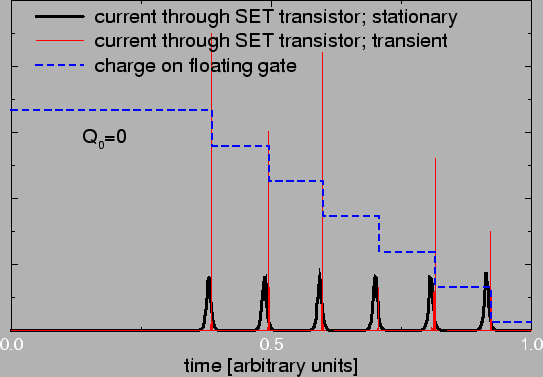
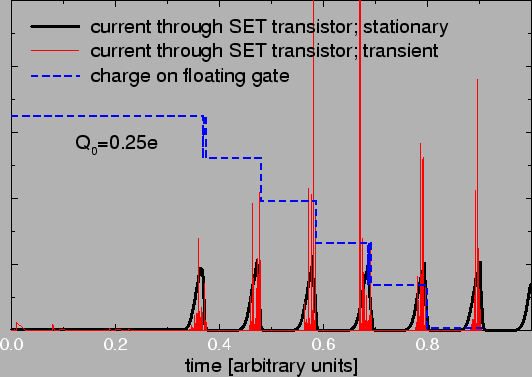
To show the random background charge independence of the Q₀-independent memory of Fig. 5.12, we give in Fig. 5.15 the current through the SET transistor for zero background charge and in Fig. 5.16 the current for non-zero background charge.

  

Figure 5.15: Discharging the floating gate of the Q₀-independent memory for Q₀ = 0. The oscillating current is clearly visible.

In both

  

Figure 5.16: Discharging the floating gate of the Q₀-independent memory for Q₀ = 0.25e. Despite background charge, the oscillating current is clearly visible

cases the Coulomb oscillations are clearly visible. Fig. 5.17 shows that the Coulomb blockade of a multi-island memory is more or less independent of random background charge and similar to that of a single island transistor consisting of two tunnel junctions.

An important issue for the fabrication and the achievable integration density (bits/ $\mbox{cm}^{2}$) is the    complexity and size of the various memory cells. The SET flip-flop shows a high complexity with 10 elements (6 tunnel junctions and 4 capacitors) with varying element parameters, or in the case of the complementary design even 14 elements (8 tunnel junctions and 6 capacitors). Ring memory, ring-trap memory, and multi-tunnel-junction memory, with 12, 13, and 7 elements respectively, are simpler in design. Their elements have similar parameters and the interconnection is considerably less complex. Especially in the case of the multi-tunnel-junction memory the connection problem is considerably reduced, since only one island has to be connected to the outside, and the number of tunnel junctions is not crucial. The Q₀-independent memory has only 4 elements (2 tunnel junctions, a floating gate and a port to the floating gate) plus a FET sense amplifier which can be responsible for many memory cells. The simplest design is the multi-island memory cell which needs a small area of granular film and a drain, source and gate electrode.

Considering the multi-island memory design, cell sizes of 50 nm $\times$50 nm and below are possible, which would result in an integration density of $4\cdot 10^{10}$ bits/ $\mbox{cm}^{2}$.

  

Figure 5.17: I-V characteristics of single island SET transistor and multiple island SET transistor consisting of 50 islands.