Next: C.2 The Finite Potential
Up: C Solutions to Schrödinger's
Previous: C Solutions to Schrödinger's
C.1 The Infinite Potential Well
The infinite potential well is a simple model for a
quantum dot (see
Fig. C.1).
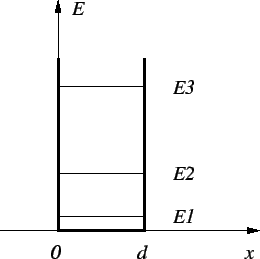
Figure C.1:
The infinite potential well of width d.
 |
We are interested in the characteristic spacing
between energy levels, especially the height of the first level.
Starting with the Ansatz
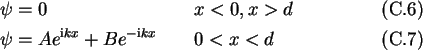
and the boundary conditions

non-trivial solutions are only possible for discrete
wave vector values

And consequently the energy levels are
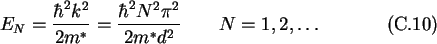
Christoph Wasshuber