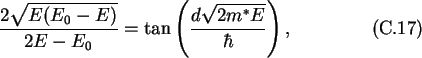Next: C.3 The Rectangular Potential
Up: C Solutions to Schrödinger's
Previous: C.1 The Infinite Potential
C.2 The Finite Potential Well
To show that the infinite well approximation is sufficient in our case, the
energy levels of a finite potential well, Fig. C.2, are calculated
and compared to (C.10).
Figure C.2:
Finite potential well with width d and height E0.
On the right side a comparison of the first ten energy levels for an
infinite potential well of width 10 nm and a finite well with the same width
and a height of 0.34 eV is shown. The first levels differ only slightly.
 |
The Ansatz for the three regions is
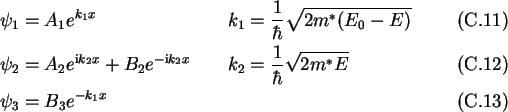
The boundary conditions yield the following equations:
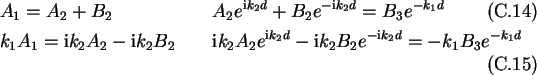
Solving for A2 gives
![\begin{gather}A_2\left[\left(1+\frac{\text{i}k_2}{k_1}\right)^2e^{\text{i}k_2d}-
\left(1-\frac{\text{i}k_2}{k_1}\right)^2e^{-\text{i}k_2d}\right]=0
\end{gather}](img403.gif)
Since the trivial solution A2=0 is not of interest, the second term has
to be zero. This is the condition fulfilled only for special energies.
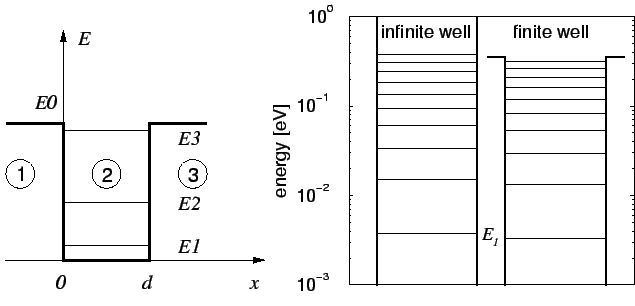
The transcendent condition can be written as
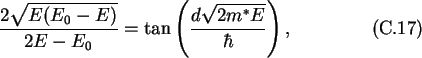
which is only numerically solvable. A quantitative comparison is given for
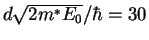 ,
which corresponds to a well with a
width of 10 nm and a height of 0.34 eV, in the right side of
Fig. C.2. The first energy levels differ only slightly.
,
which corresponds to a well with a
width of 10 nm and a height of 0.34 eV, in the right side of
Fig. C.2. The first energy levels differ only slightly.




Next: C.3 The Rectangular Potential
Up: C Solutions to Schrödinger's
Previous: C.1 The Infinite Potential
Christoph Wasshuber


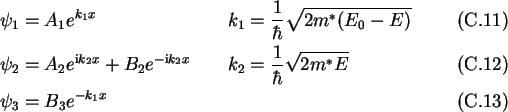
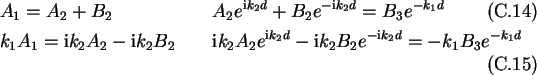
![\begin{gather}A_2\left[\left(1+\frac{\text{i}k_2}{k_1}\right)^2e^{\text{i}k_2d}-
\left(1-\frac{\text{i}k_2}{k_1}\right)^2e^{-\text{i}k_2d}\right]=0
\end{gather}](img403.gif)