|
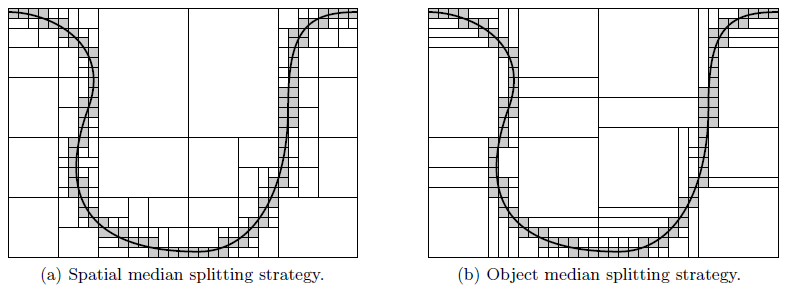
Different splitting strategies have been proposed to reduce the average number of traversed boxes [39,72]. Among the simplest are the spatial median (SM) and the object median (OM) splitting strategy. The first algorithm chooses the splitting plane in such a way that the box is separated into two boxes of approximately equal size. The second algorithm uses the OM instead, which attempts to create boxes containing approximately the same number of objects. The objects are in this case the non-empty cells. Figure 5.3 shows the corresponding spatial subdivisions for both strategies.

|
A much better strategy was presented in [72], which explicitly attempts to reduce the average number of traversed subboxes. The surface area heuristic (SAH) strategy uses a cost model to decide which splitting plane is best. For the following considerations all rays are assumed to be uniformly distributed. This corresponds to an arriving flux distribution at
![]() , which obeys the most frequently used directional distribution, the cosine distribution (2.5). Furthermore, the cost for a complete traversal through
, which obeys the most frequently used directional distribution, the cosine distribution (2.5). Furthermore, the cost for a complete traversal through
![]() is considered, which is not the case in reality, because particles are only tracked, until they reach the surface.
is considered, which is not the case in reality, because particles are only tracked, until they reach the surface.
According to geometric probability theory [102], a uniformly distributed ray which intersects
![]() , also intersects another axis-aligned box
, also intersects another axis-aligned box
![]() with
with
![]() with a probability of
with a probability of
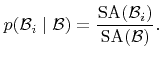 |
(5.22) |
Consider a box
![]() during setup of the spatial subdivision, which needs to be split further. This is the case, if
during setup of the spatial subdivision, which needs to be split further. This is the case, if
![]() is still larger than a grid cell and contains at least one non-empty cell. Let
is still larger than a grid cell and contains at least one non-empty cell. Let
![]() be the number of non-empty grid cells in
be the number of non-empty grid cells in
![]() which is subdivided along a certain plane into boxes
which is subdivided along a certain plane into boxes
![]() and
and
![]() , which then contain
, which then contain ![]() and
and ![]() (with
(with
![]() ) non-empty grid cells, respectively. The additional costs are reduced, if the expression
) non-empty grid cells, respectively. The additional costs are reduced, if the expression
For good splitting strategies, such as the SAH, a logarithmic scaling with the number of objects can be observed for the average number of traversed boxes (5.23) [39]. Here the objects correspond to the non-empty cells which scale linearly with the surface size. Hence, as already stated in Section 5.2.4, the expected computational complexity of ray tracing is in the order of
![]() where
where
![]() is a measure of the surface size.
is a measure of the surface size.