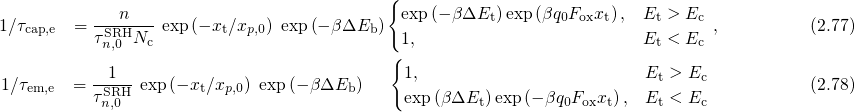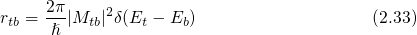
Up to this point, trapping has been defined for transitions from one band state in the substrate into one trap state or vice versa. Each of the possible transitions is associated with one rate entering the trapping dynamics. In order to reduce the set of rate equations, compact analytical expressions for the overall trapping rates into one defect are required. In this section, a derivation of the sought expressions will be presented for the case of elastic as well as inelastic tunneling.
The derivation below follows the approach of Tewksbury [23] with some slight modifications. For a proper description of charge trapping, Fermi’s golden rule is taken as a starting point. This fundamental law (see Appendix A.1) gives the rate for a transition between a certain initial and final state. In its most general form it reads:
The subscripts and
and  denote a trap or a band state, respectively, and
denote a trap or a band state, respectively, and  represents the tunneling matrix element. The
represents the tunneling matrix element. The 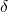 -function indicates that the
electron energy before and after the transition must be conserved as it is
required for elastic tunneling. In semiconductor devices, the charge carriers
captured in the dielectric can originate from several different energy levels of the
substrate valence or conduction band. In order to account for their contribution
to the whole tunneling rate, the sum over all
-function indicates that the
electron energy before and after the transition must be conserved as it is
required for elastic tunneling. In semiconductor devices, the charge carriers
captured in the dielectric can originate from several different energy levels of the
substrate valence or conduction band. In order to account for their contribution
to the whole tunneling rate, the sum over all 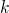 states has to be taken.
Here,
states has to be taken.
Here, 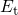 and
and 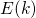 is the trap level and the electron energy in the substrate,
respectively. The subscript
is the trap level and the electron energy in the substrate,
respectively. The subscript 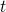 in equation (2.33) has been omitted since only
tunneling into and out of a certain trap is considered. The matrix element
in equation (2.33) has been omitted since only
tunneling into and out of a certain trap is considered. The matrix element 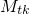 involves the trap wavefunction, whose exact form is in general unknown. Often, the
calculation of the matrix element is simplified to a one-dimensional
involves the trap wavefunction, whose exact form is in general unknown. Often, the
calculation of the matrix element is simplified to a one-dimensional 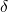 -type trap
potential. Its solution [23], consists of the factors
-type trap
potential. Its solution [23], consists of the factors 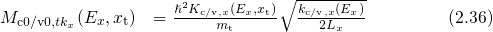
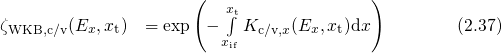
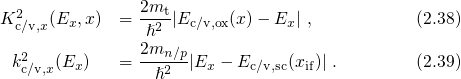
 ’ and ‘
’ and ‘ ’, accordingly. The second factor
’, accordingly. The second factor 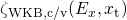 of the matrix element in equation (2.35) arises from the exponential decay of the
electron wavefunction, which can be derived using the WKB approximation. Since
this factor shows a dependence on the carrier kinetic energy
of the matrix element in equation (2.35) arises from the exponential decay of the
electron wavefunction, which can be derived using the WKB approximation. Since
this factor shows a dependence on the carrier kinetic energy 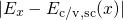 perpendicular to the interface, the summation over all band states must be split
into a one-dimensional and a two-dimensional part (see Appendix A.4):
perpendicular to the interface, the summation over all band states must be split
into a one-dimensional and a two-dimensional part (see Appendix A.4):
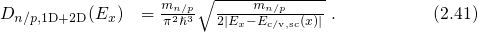
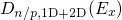 a factor of two has been introduced in order to account for spin
degeneracy. Note that the DOS has been derived based on the parabolic band
approximation, however, the potential well in the inversion layer gives rise to the
formation of subbands (see Section 2.1) and in consequence a different DOS. This
means that the equation (2.40) neglects quantization effects in the inversion
layer. Nevertheless, inserting the expression (2.40) into equation (2.34) yields
which can be simplified to The factor
a factor of two has been introduced in order to account for spin
degeneracy. Note that the DOS has been derived based on the parabolic band
approximation, however, the potential well in the inversion layer gives rise to the
formation of subbands (see Section 2.1) and in consequence a different DOS. This
means that the equation (2.40) neglects quantization effects in the inversion
layer. Nevertheless, inserting the expression (2.40) into equation (2.34) yields
which can be simplified to The factor 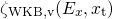 enters the above equation as a square, which corresponds
to a transmission coefficient of an electron through an energy barrier [126], and will
be referred to as the ‘WKB factor’ in the following.
enters the above equation as a square, which corresponds
to a transmission coefficient of an electron through an energy barrier [126], and will
be referred to as the ‘WKB factor’ in the following.
In this derivation, the calculation of the matrix element has been reduced to a
one-dimensional problem in favor of a compact and analytical expression. In order to
correct for this approximation, the term 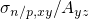 must be introduced following
Freeman’s approach [103].
must be introduced following
Freeman’s approach [103].
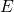 coincides with the trap level
coincides with the trap level 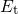 — even though
— even though 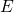 can have different components
can have different components
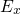 . In this derivation, the cross-sections
. In this derivation, the cross-sections 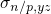 correspond to fitting parameters
but can be estimated by analytical expressions presented in [23]. Since the values
obtained by these expressions range around
correspond to fitting parameters
but can be estimated by analytical expressions presented in [23]. Since the values
obtained by these expressions range around 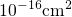 and are subject to small
variations, the cross-sections are assumed to be constant throughout this
thesis.
and are subject to small
variations, the cross-sections are assumed to be constant throughout this
thesis.
Compact expressions for inelastic transitions are provided by the framework of the Shockley-Read-Hall (SRH) theory [127]. It has been developed to describe recombination centers in bulk but has also been extended for the case of electron or hole trapping into dielectrics [128]. The following derivation of the SRH rates is generalized to NMP transitions, presuming the case of hole trapping, and starts from equation (2.27).
The trap and the band state involved in the NMP transition are labeled by the subscripts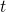 and
and 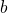 , respectively.
, respectively. 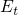 denotes the thermodynamic trap level and
denotes the thermodynamic trap level and
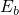 an arbitrary state in the valence band. Since the NMP theory assumes thermal
transitions, the energies of the states
an arbitrary state in the valence band. Since the NMP theory assumes thermal
transitions, the energies of the states 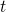 and
and 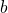 may differ, meaning that the trap
can in principle exchange charge carriers with the entire valence band. In order
to account for this fact, a sum over all band states has to be carried out.
may differ, meaning that the trap
can in principle exchange charge carriers with the entire valence band. In order
to account for this fact, a sum over all band states has to be carried out.
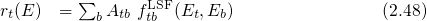
 can be approximated by an integral over the valence band DOS
can be approximated by an integral over the valence band DOS
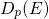 , where
, where  can be identified with the energy
can be identified with the energy 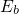 of the valence band state
of the valence band state
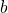 (see Appendix A.4). Using the expression (2.49), the transition rate can be rewritten as
(see Appendix A.4). Using the expression (2.49), the transition rate can be rewritten as 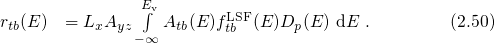
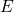 is empty.
The first condition is considered by the trap occupancy
is empty.
The first condition is considered by the trap occupancy 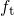 . The second one can be
expressed by
. The second one can be
expressed by 
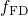 being the Fermi-Dirac distribution
being the Fermi-Dirac distribution 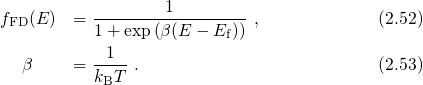
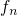 equals the Fermi-Dirac distribution
equals the Fermi-Dirac distribution 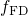 . Combining the rate
equations for hole capture (2.54) and emission (2.55) and using the shorthands
. Combining the rate
equations for hole capture (2.54) and emission (2.55) and using the shorthands
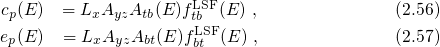
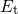 is occupied according to
the Fermi-Dirac statistics
is occupied according to
the Fermi-Dirac statistics 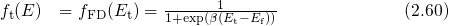

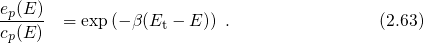
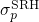 and the thermal velocity
and the thermal velocity 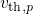 . The
definition of the hole emission time constant follows from equation (2.64).
. The
definition of the hole emission time constant follows from equation (2.64).
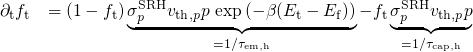
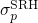 in equation
(2.65) contains the matrix element
in equation
(2.65) contains the matrix element 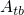 and the Frank-Condon factor
and the Frank-Condon factor 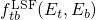 .
The former is associated with an electron tunneling process and thus often
approximated by a WKB factor. The latter is strongly determined by the barrier
height of an NMP transition (see Section 2.4). This suggests that also the cross
section
.
The former is associated with an electron tunneling process and thus often
approximated by a WKB factor. The latter is strongly determined by the barrier
height of an NMP transition (see Section 2.4). This suggests that also the cross
section 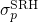 in the SRH theory should somehow reflect this barrier dependence.
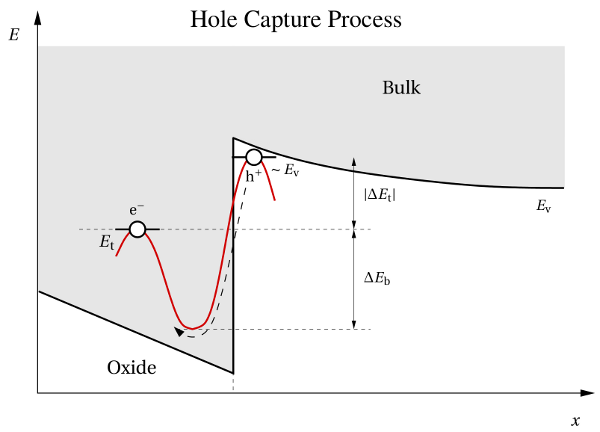
For a hole capture process with
in the SRH theory should somehow reflect this barrier dependence.
For a hole capture process with 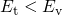 (cf. Fig. 2.5), the barrier height can be
split into two components, namely
(cf. Fig. 2.5), the barrier height can be
split into two components, namely 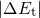 and
and 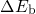 . The former is defined as
where
. The former is defined as
where 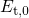 and
and 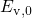 are the trap level and the valence band edge in the absence of
an electric field. The value of
are the trap level and the valence band edge in the absence of
an electric field. The value of 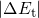 corresponds to minimal energy required for a
transition. The latter, that is
corresponds to minimal energy required for a
transition. The latter, that is 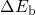 , represents only the remainder to the overall
barrier
, represents only the remainder to the overall
barrier 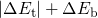 . For the
. For the 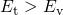 , the component
, the component 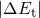 vanishes and only
vanishes and only
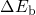 remains. Using the above definitions of the barriers, the cross section can be
written as where
remains. Using the above definitions of the barriers, the cross section can be
written as where  and
and 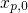 denote a temperature-independent cross section and the
characteristic tunneling length. It is remarked at this point that the transition
barriers has been assumed to be independent of the energy of the holes.
denote a temperature-independent cross section and the
characteristic tunneling length. It is remarked at this point that the transition
barriers has been assumed to be independent of the energy of the holes.
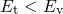 .
The hole is initially located in the bulk at an energy level
.
The hole is initially located in the bulk at an energy level 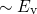 . Its capture
can be imagined to proceed over a downwards directed barrier of the height
. Its capture
can be imagined to proceed over a downwards directed barrier of the height
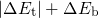 . For this process, an minimum energy of
. For this process, an minimum energy of 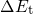 is required to
push down the hole from
is required to
push down the hole from 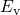 to
to 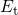 . As a consequence, the forward barrier
is higher than its reverse counterpart by a value of
. As a consequence, the forward barrier
is higher than its reverse counterpart by a value of 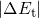 . The rest of the
barrier height is accounted for by
. The rest of the
barrier height is accounted for by 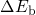 , which is assumed to have a finite
value for generality. It is noted here that the SRH theory [127] has been derived
without assuming thermal barriers. Therefore, this theory is usually considered
for processes proceeding without or with a negligible thermal barrier.
, which is assumed to have a finite
value for generality. It is noted here that the SRH theory [127] has been derived
without assuming thermal barriers. Therefore, this theory is usually considered
for processes proceeding without or with a negligible thermal barrier.Making use of
with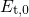 and
and 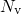 being the trap level in the flat band case and the effective
valence band weights, respectively, the rates (2.69) and (2.70) can be rewritten as
with The corresponding expression for electron trapping from the conduction band can be
derived in an analogous manner and reads
being the trap level in the flat band case and the effective
valence band weights, respectively, the rates (2.69) and (2.70) can be rewritten as
with The corresponding expression for electron trapping from the conduction band can be
derived in an analogous manner and reads