3.3 Density Functional Theory
3.3.1 Introduction
In material science, numerous research topics are related to microscopic processes.
The description of these processes often relies on quantities which are not assessable
by experiments but can be extracted from atomistic simulations. In the past,
so-called first-principles calculations have been successfully employed for the
determination of those quantities. These calculations solve the Schrödinger equation
of the electrons for a given atomic configuration, and therefore, they do not
depend on any fitting parameters. At this point it is should be noted that
the knowledge about the exact atomic configuration is often vague, which
can sometimes be an serious issue. For instance, it is frequently debated
whether the 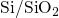 interface is abrupt or graded or even has defects,
such as suboxides or protrusions. One prominent example of first principle
calculations is the Hartree-Fock method. It takes the fundamental exchange
interactions
into account but suffers from a complete neglect of electron correlations and thus fails
to reproduce some fundamental properties in solid state physics. Since Hartree-Fock
simulations scale badly with the number of electrons, they perform unsatisfactorily
with respect to the computational costs when more than only a few tens
of atoms are considered. Therefore an alternative approach based on the
electron density has been pursued. It is termed density functional theory
(DFT) [136, 91, 92] and can be considered as the workhorse in the field of
microscopic simulations. In the following, the basics of this method will be
explained.
interface is abrupt or graded or even has defects,
such as suboxides or protrusions. One prominent example of first principle
calculations is the Hartree-Fock method. It takes the fundamental exchange
interactions
into account but suffers from a complete neglect of electron correlations and thus fails
to reproduce some fundamental properties in solid state physics. Since Hartree-Fock
simulations scale badly with the number of electrons, they perform unsatisfactorily
with respect to the computational costs when more than only a few tens
of atoms are considered. Therefore an alternative approach based on the
electron density has been pursued. It is termed density functional theory
(DFT) [136, 91, 92] and can be considered as the workhorse in the field of
microscopic simulations. In the following, the basics of this method will be
explained.
3.3.2 The Basic Concepts of DFT
The first main idea of DFT is to reformulate the energy of an atomic system
as a functional of the ground state electron density instead of the electron
wavefunction. The proof of existence for such functionals relies on a one-to-one
correspondence between the external potential 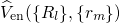 and the
ground state electron density
and the
ground state electron density 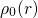 . The mapping of
. The mapping of 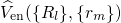 onto
onto
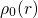 is obvious: Any Hamiltonian
is obvious: Any Hamiltonian 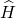 with a given external potential
with a given external potential
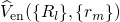 has a ground state solution with an
has a ground state solution with an 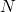 -electron wavefunctions
-electron wavefunctions
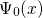 , which can be uniquely identified with an electron density
, which can be uniquely identified with an electron density 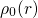 using
using
The other direction of this mapping (see Fig. 3.3) was proven by the Hohenberg-Kohn
(HK) theorem [137]. Due to the resulting one-to-one correspondence between
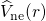 and
and 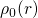 , the energy of the atomic system
, the energy of the atomic system 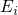 can be expressed as a
functional of the electron density
can be expressed as a
functional of the electron density 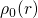 . Note that DFT is actually restricted to
so-called ‘V-representable’ electron densities, however, this is not an issue in the
practical use.
. Note that DFT is actually restricted to
so-called ‘V-representable’ electron densities, however, this is not an issue in the
practical use.
The many-electron wavefunction used in equation (3.26) reads
where its form depends on the ‘combination’ of all spatial electron coordinates.
Unfortunately, such an approach would by far exceed any computational capabilities.
However, this problem can be overcome using the Kohn-Sham (KS) ansatz, in which
the fully-interacting system is replaced by a non-interacting one. This ansatz
corresponds to a mean-field approach, where the wavefunction is decomposed into a
product of single-electron orbitals 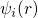 . This simplification leads to a neglect of an
energy contribution termed ‘correlations’. As a correction, the functional
. This simplification leads to a neglect of an
energy contribution termed ‘correlations’. As a correction, the functional ![Ecx[ρ(r)]](diss1428x.png) must be introduced as an additional term in the Hamiltonian. It is noted
that this term does not only account for the correlations but also for the
unconsidered exchange interactions. Applying the variation principle to the
modified Hamiltonian yields a single-particle Schrödinger equation, also
referred to as Kohn-Sham equation in DFT. This equation includes an effective
potential
must be introduced as an additional term in the Hamiltonian. It is noted
that this term does not only account for the correlations but also for the
unconsidered exchange interactions. Applying the variation principle to the
modified Hamiltonian yields a single-particle Schrödinger equation, also
referred to as Kohn-Sham equation in DFT. This equation includes an effective
potential 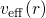 , which is produced by the Coulomb forces of all other
electrons and nuclei and incorporates the exchange and correlation interactions.
The Kohn-Sham orbitals
, which is produced by the Coulomb forces of all other
electrons and nuclei and incorporates the exchange and correlation interactions.
The Kohn-Sham orbitals 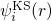 only reproduce the correct electron density but
actually have no physical meaning. The total energy of the atomic system
reads:
Up to now, DFT has been presented as a formally exact framework, however, the
complicated part of physics, namely the exchange and correlation interactions, is
incorporated in
only reproduce the correct electron density but
actually have no physical meaning. The total energy of the atomic system
reads:
Up to now, DFT has been presented as a formally exact framework, however, the
complicated part of physics, namely the exchange and correlation interactions, is
incorporated in ![Exc[ρ(r)]](diss1434x.png) . The above eigen-value problem is solved using an
iterative method that makes up the computationally expensive step of the DFT
calculations. A schematic representation of a self-consistent loop in this numerical
method is depicted in Fig. 3.4. With the forces at hands, the energy of a
configuration can be minimized with respected to the atomic coordinates.
Mathematically, this corresponds to finding the stationary point of a function whose
exact form is generally unknown. This task is solved employing iterative
methods [92], such as quasi-Newton methods or the conjugate gradient method for
instance. The obtained energy minima corresponds to the stable configurations,
which are physically realized and thus important for the determination of stable
defect configurations.
. The above eigen-value problem is solved using an
iterative method that makes up the computationally expensive step of the DFT
calculations. A schematic representation of a self-consistent loop in this numerical
method is depicted in Fig. 3.4. With the forces at hands, the energy of a
configuration can be minimized with respected to the atomic coordinates.
Mathematically, this corresponds to finding the stationary point of a function whose
exact form is generally unknown. This task is solved employing iterative
methods [92], such as quasi-Newton methods or the conjugate gradient method for
instance. The obtained energy minima corresponds to the stable configurations,
which are physically realized and thus important for the determination of stable
defect configurations.
When self-consistency is achieved for this loop, the electronic part of the system is
solved. However, the nuclear part described by the Schrödinger equation
(2.17) has not been addressed so far. Due to the relatively high nuclei mass,
quantum mechanical considerations can be neglected so that the Schrödinger
equation (2.17) can be replaced by Newton’s law of motion. The required
forces are evaluated according to the Hellmann-Feynman theorem [91, 92]:
3.3.3 Simulation Details
The simulations in this thesis are performed using the Vienna Ab-initio
Simulation Package (VASP) [138, 139, 140, 141], which is based on a plane-wave
implementation of DFT. The computational details, especially those important for
defect calculations, will be discussed in the following.
The correct description of the exchange-correlation functional takes a crucial role in
DFT. The local-density approximation has already achieved satisfactory results for
systems with a slowly varying electron density, such as metals [93]. However, it has a
tendency termed overbinding, which overestimate binding energies and thus for
instance predicts too strong hydrogen bonds with too short bonds lengths. The
generalized gradient approximation is a systematic expansion, gives good
results in most cases, and corrects for the overbinding [93]. Recently, hybrid
functionals [142] have emerged, which achieve an improved accuracy, especially for
the bandgap [143]. However, their use for large-scale investigations of atomic systems
is time-demanding. Therefore, the functional based on the parametrization of
Perdew, Burke, and Ernzerhof [144] and provided by the VASP code has
been regarded as a reasonable trade-off between accuracy and computation
time.
A realistic defect model must contain some of the surrounding atoms of its host
material since the atoms of a real defect are connected to the surrounding atomic
network and thus are not allowed to move around freely. In order to account for this,
the long-range structural relaxations are handled using periodic supercells
containing 108 atoms. The host structures have been produced using empirical
potential molecular dynamics presented in Section 3.4. The resulting structures
were optimized on DFT level employing a conjugate gradient algorithm
that minimizes the force on each atom below 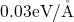 . In a further step,
the defects were manually introduced by the addition or removal of single
atoms, followed by a subsequent structural optimization. Due to the imposed
periodic boundary conditions in supercells, the Kohn-Sham orbitals
. In a further step,
the defects were manually introduced by the addition or removal of single
atoms, followed by a subsequent structural optimization. Due to the imposed
periodic boundary conditions in supercells, the Kohn-Sham orbitals 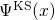 were represented by an expansion of plane waves up to a cut-off energy of
were represented by an expansion of plane waves up to a cut-off energy of
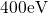 . Since the large size of the supercells (
. Since the large size of the supercells (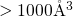 ) decreases the
corresponding Brillouin zones, the
) decreases the
corresponding Brillouin zones, the 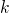 -point sampling was restricted to the
-point sampling was restricted to the 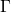 -point
only.
-point
only.
VASP employs a sophisticated transformation of the Kohn-Sham equations based on
the projector-augmented wave (PAW) method [145, 146], which smoothens the
effective potential 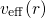 near the cores in order to spare the computationally
expensive inclusion of the highly oscillating wavefunctions. The PAW method is one
of the most powerful approaches which combines a good transferability to
different atomistic configurations and chemical compositions with the required
accuracy [145, 93].
near the cores in order to spare the computationally
expensive inclusion of the highly oscillating wavefunctions. The PAW method is one
of the most powerful approaches which combines a good transferability to
different atomistic configurations and chemical compositions with the required
accuracy [145, 93].
Defect levels for charge capture or emission are calculated by means of the formation
energies ![U q[Xq ]
f](diss1447x.png) [147, 148], which are defined for a certain charge state
[147, 148], which are defined for a certain charge state 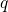 and a
certain atomic configuration
and a
certain atomic configuration 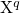 of the defect as
of the defect as
![Etot[bulk]](diss1451x.png) stands for the total energy of a supercell containing pure bulk material
while
stands for the total energy of a supercell containing pure bulk material
while ![Etot[Xq′]](diss1452x.png) the supercell also contains the defect. The third term in equation
(3.32) corrects for the different numbers of atoms in both supercells.
the supercell also contains the defect. The third term in equation
(3.32) corrects for the different numbers of atoms in both supercells. 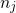 gives the
number of added (
gives the
number of added (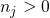 ) or removed (
) or removed (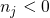 ) atoms which are required to create
the defect from a perfect bulk structure. The subscript
) atoms which are required to create
the defect from a perfect bulk structure. The subscript 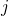 refers to the atom type
and
refers to the atom type
and  denotes the corresponding energy in an atomic reservoir, which must be
specified for each individual use case. The fourth term in equation (3.32)
accounts for the charge state
denotes the corresponding energy in an atomic reservoir, which must be
specified for each individual use case. The fourth term in equation (3.32)
accounts for the charge state 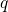 of the defect.
of the defect. 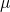 is defined as the electron
chemical potential referenced with respect to the valence band edge
is defined as the electron
chemical potential referenced with respect to the valence band edge 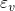 in a
bulk-like region.
in a
bulk-like region. 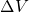 [147] corrects the shift in the reference level between
two differently charged supercells and is obtained from the difference in the
electrostatic potential far distant from the defect. Due to the periodic boundary
conditions, charge neutrality must be ensured within a supercell. Thus a
homogeneous compensating background charge must be introduced in calculations of
charged defects. Its artificial Coulomb interactions are corrected by the term
[147] corrects the shift in the reference level between
two differently charged supercells and is obtained from the difference in the
electrostatic potential far distant from the defect. Due to the periodic boundary
conditions, charge neutrality must be ensured within a supercell. Thus a
homogeneous compensating background charge must be introduced in calculations of
charged defects. Its artificial Coulomb interactions are corrected by the term
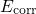 .
.
In DFT literature, one distinguishes between switching and thermodynamic
transition levels. The former pertain to a charge capture or emission process, during
which the atomic configuration is preserved, and thus they have the same meaning as
the electron capture levels and hole emission levels presented in Section 2.3. In DFT
they are defined as the difference of formation energies [113, 149] and can be written
as
Analogously to Section 2.3, energy levels 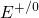 and
and 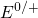 apply to a process which
neutralizes a positive defect or introduces a positive charge into a neutral defect,
respectively. An alternative possibility for the evaluation of the switching transition
levels is provided by the Slater-Janak theorem [150].
apply to a process which
neutralizes a positive defect or introduces a positive charge into a neutral defect,
respectively. An alternative possibility for the evaluation of the switching transition
levels is provided by the Slater-Janak theorem [150].
The thermodynamic transition levels correspond to the difference between two energy
minima, which is also the case for 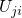 in the NMP theory (see section 2.4). In
contrast to the switching transition levels, the relaxed configurations for each charge
state must be used.
in the NMP theory (see section 2.4). In
contrast to the switching transition levels, the relaxed configurations for each charge
state must be used.
 interface is abrupt or graded or even has defects,
such as suboxides or protrusions. One prominent example of first principle
calculations is the Hartree-Fock method. It takes the fundamental exchange
interactions2
into account but suffers from a complete neglect of electron correlations and thus fails
to reproduce some fundamental properties in solid state physics. Since Hartree-Fock
simulations scale badly with the number of electrons, they perform unsatisfactorily
with respect to the computational costs when more than only a few tens
of atoms are considered. Therefore an alternative approach based on the
electron density has been pursued. It is termed density functional theory
(DFT) [136, 91, 92] and can be considered as the workhorse in the field of
microscopic simulations. In the following, the basics of this method will be
explained.
interface is abrupt or graded or even has defects,
such as suboxides or protrusions. One prominent example of first principle
calculations is the Hartree-Fock method. It takes the fundamental exchange
interactions2
into account but suffers from a complete neglect of electron correlations and thus fails
to reproduce some fundamental properties in solid state physics. Since Hartree-Fock
simulations scale badly with the number of electrons, they perform unsatisfactorily
with respect to the computational costs when more than only a few tens
of atoms are considered. Therefore an alternative approach based on the
electron density has been pursued. It is termed density functional theory
(DFT) [136, 91, 92] and can be considered as the workhorse in the field of
microscopic simulations. In the following, the basics of this method will be
explained.
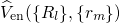 and the
ground state electron density
and the
ground state electron density 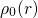 . The mapping of
. The mapping of 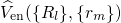 onto
onto
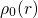 is obvious: Any Hamiltonian
is obvious: Any Hamiltonian 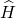 with a given external potential
with a given external potential
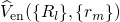 has a ground state solution with an
has a ground state solution with an  -electron wavefunctions
-electron wavefunctions
 , which can be uniquely identified with an electron density
, which can be uniquely identified with an electron density  using
using
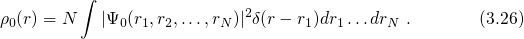
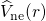 and
and 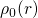 , the energy of the atomic system
, the energy of the atomic system 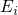 can be expressed as a
functional of the electron density
can be expressed as a
functional of the electron density 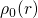 . Note that DFT is actually restricted to
so-called ‘V-representable’ electron densities, however, this is not an issue in the
practical use.
. Note that DFT is actually restricted to
so-called ‘V-representable’ electron densities, however, this is not an issue in the
practical use.

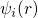 . This simplification leads to a neglect of an
energy contribution termed ‘correlations’. As a correction, the functional
. This simplification leads to a neglect of an
energy contribution termed ‘correlations’. As a correction, the functional ![Ecx[ρ(r)]](diss1428x.png) must be introduced as an additional term in the Hamiltonian. It is noted
that this term does not only account for the correlations but also for the
unconsidered exchange interactions. Applying the variation principle to the
modified Hamiltonian yields a single-particle Schrödinger equation, also
referred to as Kohn-Sham equation in DFT. This equation includes an effective
potential
must be introduced as an additional term in the Hamiltonian. It is noted
that this term does not only account for the correlations but also for the
unconsidered exchange interactions. Applying the variation principle to the
modified Hamiltonian yields a single-particle Schrödinger equation, also
referred to as Kohn-Sham equation in DFT. This equation includes an effective
potential 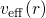 , which is produced by the Coulomb forces of all other
electrons and nuclei and incorporates the exchange and correlation interactions.
, which is produced by the Coulomb forces of all other
electrons and nuclei and incorporates the exchange and correlation interactions.
![( 2 )
- ℏ2me-∇2 +veff(r) ψKiS(r) = εKiS ψKiS(r) (3.28)
∫ ′
veff(r) = Ven(r)+ ρ0(r)′-dr′+ δ-Exc[ρ0(r)] (3.29)
◟--|r--◝◜r|-◞ ◟--δρ◝(r◜)--◞
=Vee(r) =Vxc(r)](diss1430x.png)
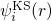 only reproduce the correct electron density but
actually have no physical meaning. The total energy of the atomic system
reads
only reproduce the correct electron density but
actually have no physical meaning. The total energy of the atomic system
reads![occ ∫ ∫ ∫
∑ KS 1 ρ0(r)ρ0(r′) ′
Ei[ρ0(r)] = εi - 2 |r- r′| drdr- Vxc(r)ρ0(r)dr+ Exc[ρ0(r)] (3.30)
i](diss1433x.png)
![Exc[ρ(r)]](diss1434x.png) . The above eigen-value problem is solved using an
iterative method that makes up the computationally expensive step of the DFT
calculations. A schematic representation of a self-consistent loop in this numerical
method is depicted in Fig. 3.4. With the forces at hands, the energy of a
configuration can be minimized with respected to the atomic coordinates.
Mathematically, this corresponds to finding the stationary point of a function whose
exact form is generally unknown. This task is solved employing iterative
methods
. The above eigen-value problem is solved using an
iterative method that makes up the computationally expensive step of the DFT
calculations. A schematic representation of a self-consistent loop in this numerical
method is depicted in Fig. 3.4. With the forces at hands, the energy of a
configuration can be minimized with respected to the atomic coordinates.
Mathematically, this corresponds to finding the stationary point of a function whose
exact form is generally unknown. This task is solved employing iterative
methods 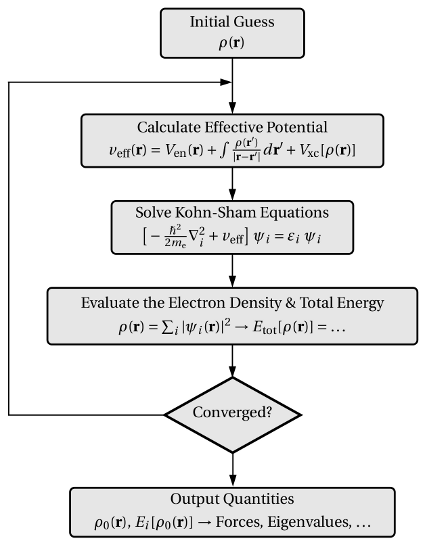
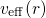 ,
the diagonalization of the Kohn-Sham equations, and the subsequent evaluation
of
,
the diagonalization of the Kohn-Sham equations, and the subsequent evaluation
of 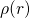 along with
along with  . As long as the convergence criterion is not fulfilled,
the numerical procedure is continued with the last
. As long as the convergence criterion is not fulfilled,
the numerical procedure is continued with the last 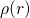 instead of the initial
guess. When the criterion is satisfied, various output quantities are computed.
instead of the initial
guess. When the criterion is satisfied, various output quantities are computed.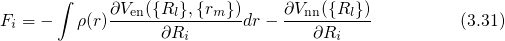
 . In a further step,
the defects were manually introduced by the addition or removal of single
atoms, followed by a subsequent structural optimization. Due to the imposed
periodic boundary conditions in supercells, the Kohn-Sham orbitals
. In a further step,
the defects were manually introduced by the addition or removal of single
atoms, followed by a subsequent structural optimization. Due to the imposed
periodic boundary conditions in supercells, the Kohn-Sham orbitals 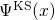 were represented by an expansion of plane waves up to a cut-off energy of
were represented by an expansion of plane waves up to a cut-off energy of
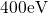 . Since the large size of the supercells (
. Since the large size of the supercells (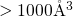 ) decreases the
corresponding Brillouin zones, the
) decreases the
corresponding Brillouin zones, the 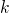 -point sampling was restricted to the
-point sampling was restricted to the 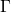 -point
only.
-point
only.
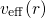 near the cores in order to spare the computationally
expensive inclusion of the highly oscillating wavefunctions. The PAW method is one
of the most powerful approaches which combines a good transferability to
different atomistic configurations and chemical compositions with the required
accuracy
near the cores in order to spare the computationally
expensive inclusion of the highly oscillating wavefunctions. The PAW method is one
of the most powerful approaches which combines a good transferability to
different atomistic configurations and chemical compositions with the required
accuracy ![U q[Xq ]
f](diss1447x.png)
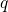 and a
certain atomic configuration
and a
certain atomic configuration 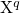 of the defect as
of the defect as ![′ ′ ∑
Uqf [Xq] = Etot[Xq ]- Etot[bulk]- njηj + q(μ + εv + ΔV )+ Ecorr . (3.32)
j](diss1450x.png)
![Etot[bulk]](diss1451x.png) stands for the total energy of a supercell containing pure bulk material
while
stands for the total energy of a supercell containing pure bulk material
while ![Etot[Xq′]](diss1452x.png) the supercell also contains the defect. The third term in equation
(3.32) corrects for the different numbers of atoms in both supercells.
the supercell also contains the defect. The third term in equation
(3.32) corrects for the different numbers of atoms in both supercells. 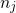 gives the
number of added (
gives the
number of added (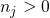 ) or removed (
) or removed (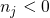 ) atoms which are required to create
the defect from a perfect bulk structure. The subscript
) atoms which are required to create
the defect from a perfect bulk structure. The subscript 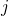 refers to the atom type
and
refers to the atom type
and  denotes the corresponding energy in an atomic reservoir, which must be
specified for each individual use case. The fourth term in equation (3.32)
accounts for the charge state
denotes the corresponding energy in an atomic reservoir, which must be
specified for each individual use case. The fourth term in equation (3.32)
accounts for the charge state 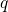 of the defect.
of the defect. 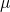 is defined as the electron
chemical potential referenced with respect to the valence band edge
is defined as the electron
chemical potential referenced with respect to the valence band edge 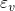 in a
bulk-like region.
in a
bulk-like region. 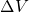
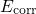 .
.
![E+ ∕0 = U 0f [X+ ]- U+f [X+ ] , (3.33)
E = U 0[X0 ]- U +[X0] , (3.34)
0∕+ f- - f0 -
E -∕0 = U f [X ]- U f [X ] , (3.35)
E0∕- = U -f [X0]- U0f [X0] . (3.36)](diss1463x.png)
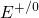 and
and 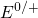 apply to a process which
neutralizes a positive defect or introduces a positive charge into a neutral defect,
respectively. An alternative possibility for the evaluation of the switching transition
levels is provided by the Slater-Janak theorem
apply to a process which
neutralizes a positive defect or introduces a positive charge into a neutral defect,
respectively. An alternative possibility for the evaluation of the switching transition
levels is provided by the Slater-Janak theorem 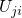 in the NMP theory (see section
in the NMP theory (see section ![ε0∕+ = E0f[X0]- E+f [X+ ] (3.37)
ε = E -[X - ]- E0[X0] (3.38)
- ∕0 f f](diss1467x.png)