2.2.3 Streuprozesse

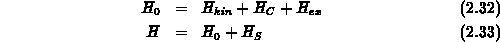
In diesem Kapitel sollen die Grundlagen der Streuprozesse abgeleitet werden. Wie bereits gezeigt worden ist, sind einige, schwache Wechselwirkungen der Ladungsträger nicht in den Bewegungsgleichungen enthalten. Stattdessen erfahren Elektronen und Löcher aufgrund dieser Prozesse eine Ablenkung und somit eine abrupte Änderung ihres Impulses. Im folgenden wird auf Wechselwirkungen von Elektronen untereinander beziehungsweise von Löchern untereinander nicht eingegangen. Ladungsträger erleiden Stöße wegen der durch thermische Bewegung der Gitterionen hervorgerufenen Störung der idealen Kristallstruktur oder aufgrund der Wechselwirkung mit ionisierten Störstellen.

Ausgehend von der separierten Schrödingergleichung 2.25 für ein Elektron sei der Hamiltonoperator wie folgt

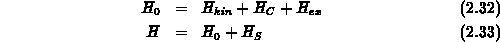
zusammengesetzt. Damit ergibt sich für die ungestörte Schrödingergleichung eines einzelnen Elektrons die folgende Form,

wobei alle Wechselwirkungen der Elektronen mit dem Kristall gering im Vergleich mit den Termen des ungestörten Hamiltonoperators seien.

Der ungestörte Zustand des Systems 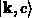, also der Einelektronenzustand 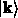und der Zustand des gesamten Kristalls 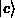werden als Produkt der Zustandsfunktion des einen Elektrons und der Zustandsfunktion des gesamten Kristalls zusammengesetzt,

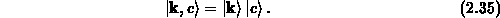
Dann kann, vorausgesetzt daß der ungestörte Hamiltonoperator zeitunabhängig und die Störung gleichfalls zeitunabhängig ist oder nur eine periodische Zeitabhängigkeit aufweist [21][43], die Übergangswahrscheinlichkeit pro Zeiteinheit 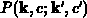eines Zustands, die von einer kleinen Störung 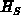hervorgerufen wird, in erster Ordnung mit der goldenen Regel von Fermi [21][35]

berechnet werden, wobei die 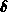-Funktion die Energieerhaltung angibt. Die Energiedifferenz des Kristalls wird dabei als 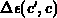bezeichnet. Im allgemeinen ist der Hamiltonoperator 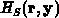eine Funktion der Raumkoordinaten des Elektrons und der augenblicklichen Verschiebung der Ionenrümpfe aus deren Gleichgewichtslage 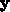. Es ist nun angebracht, die Fouriertransformierte des Hamiltonoperators bezüglich der Koordinate des Elektrons zu bilden, da der Elektronenzustand als ebene Welle angesetzt wird und der Hamiltonoperator sich in einen Term, der nur auf das Kristallsystem wirkt, und einen Term, der nur auf das Elektron wirkt, aufgespaltet werden kann. Im allgemeinen wird die Abhängigkeit vom Elektronenzustand als 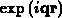angesetzt. Man erhält für den Term in spitzen Klammern vom Zustand 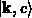in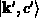

wenn über das gesamte Volumen 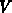des Materials integriert wird. Dabei soll die Impulserhaltung

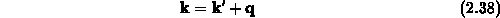
mit dem Wellenvektor des Kristalls 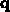erfüllt sein. Das Integral in Gleichung 2.37 wird nun mit der Transformation 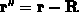umgeformt. Der Vektor 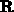führt zu einer Zelle im Raumgitter, 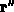gibt die Lage des Elektrons innerhalb dieser Zelle an. Außerdem sei die Wellenfunktion auf die Anzahl der Gitterzellen 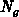normiert. Damit ergibt sich mit dem Volumen der Einheitszelle im Raumgitter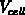

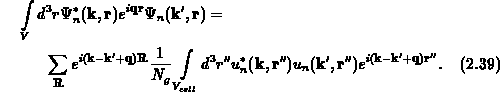
Bei näherer Betrachtung zeigt sich, daß man die Summe aller Zellen im Kristall als

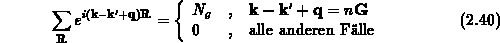
ausdrücken kann, wobei 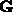ein Gittervektor des reziproken Gitters ist. Die Prozesse können nun in Normalprozeß, falls gleich Null ist oder als Umklappprozeß, falls ungleich Null ist, unterteilt werden. Faßt man nun alle Beiträge zusammen, so kann man für die Übergangswahrscheinlichkeit folgendes Ergebnis

anschreiben, wobei der Überlappungsfaktor als Integral

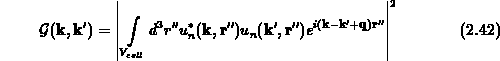
berechnet werden kann. Dieser Faktor wird, da in den meisten Fällen auch das Matrixelement 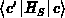nicht genau bekannt ist, bei der Berechnung der Streuraten oft vernachlässigt, als konstant angesetzt oder aber in das Matrixelement einbezogen [35][36]. Jedoch wird angenommen, daß diese Korrektur Streuprozesse bei hohen Kollisionsenergien in einem starken Ausmaß beeinflußt und von der exakten Kenntnis der Wellenfunktion abhängig ist [22]. Eine Berechnung und Auswertung dieses Integrals für einfache Bandstrukturen findet sich bei [44].

Der nächste Schritt, um die totale Streurat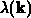e zu erhalten, besteht aus der Summation über alle Endzustände 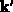. Die Summe

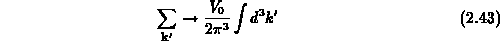
wird in ein Integral umgewandelt, und man erhält für die totale Streurate bei Verwendung der Definition von Gleichung 2.18

Eine weitere Auswertung der Streuprozesse hängt von den physikalischen Eigenschaften und von der verwendeten Bandstruktur für das jeweilige Material ab. Bei dieser Näherung erster Ordnung gilt die Energieerhaltung, und ferner hat die Wechselwirkung der Elektronen mit dem Kristall eine unendliche Lebensdauer. Eine rigorose Behandlung der Streuraten mithilfe von Green'schen Funktionen kann grundsätzlich durchgeführt werden [21], doch speziell deren Lösung mittels eines iterativen Verfahrens ist sehr rechenzeitintensiv. Für die meisten Anwendungen und wegen der hochgradigen Komplexität dieser iterativen Techniken beschränkt man sich üblicherweise auf eine Näherung erster Ordnung.

Um den Zustand des Elektrons nach der Streuung zu ermitteln, ist es notwendig, die Winkelverteilung des betrachteten Streuprozesses zu kennen. Gibt es keine Winkelabhängigkeit, so wird der Stoß isotrop verlaufen, andernfalls muß der polare Winkel gemäß dieser Verteilung berechnet werden. Der azimutale Winkel weist, da bei allen, in dieser Arbeit zu behandelnden Streumechanismen keine Abhängigkeit von diesem Winkel gegeben ist, immer eine isotrope Verteilung auf. Im nächsten Kapitel werden die einzelnen Prozesse sowohl für Silizium als auch für Siliziumdioxid diskutiert, die Streuraten und die daraus resultierende Winkelverteilung mathematisch ausgewertet.